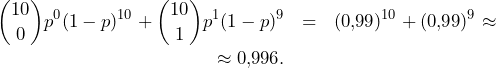Poniżej prezentujemy rozwiązania wszystkich zadań maturalnych z matematyki dla poziomu rozszerzonego (wersja arkusza w ,,formule 2023″), z którymi abiturienci mierzyli się 15. maja 2024 r. Zadania pochodzą z arkusza opublikowanego w serwisie Centralnej Komisji Egzaminacyjnej.
Zadanie 1. (0-2)
W chwili początkowej (![]() ) filiżanka z gorącą kawą znajduje się w pokoju, a temperatura
tej kawy jest równa
) filiżanka z gorącą kawą znajduje się w pokoju, a temperatura
tej kawy jest równa ![]() C. Temperatura w pokoju (temperatura otoczenia) jest stała i równa
C. Temperatura w pokoju (temperatura otoczenia) jest stała i równa ![]() C. Temperatura
C. Temperatura ![]() tej kawy zmienia się w czasie zgodnie z zależnością
tej kawy zmienia się w czasie zgodnie z zależnością
![]()
Po
Oblicz temperaturę tej kawy po następnych pięciu minutach. Wynik podaj w stopniach Celsjusza, w zaokrągleniu do jedności. Zapisz obliczenia.
Zadanie 2. (0-2)
Oblicz granicę
![]()
Zadanie 3. (0-3)
W pewnym zakładzie mleczarskim śmietana produkowana jest w ![]() -gramowych opakowaniach. Prawdopodobieństwo zdarzenia, że w losowo wybranym opakowaniu śmietana zawiera mniej niż
-gramowych opakowaniach. Prawdopodobieństwo zdarzenia, że w losowo wybranym opakowaniu śmietana zawiera mniej niż ![]() tłuszczu, jest równe
tłuszczu, jest równe ![]() . Kontroli poddajemy
. Kontroli poddajemy ![]() losowo wybranych opakowań ze śmietaną.
losowo wybranych opakowań ze śmietaną.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród opakowań
poddanych tej kontroli będzie co najwyżej jedno opakowanie ze śmietaną, które
zawiera mniej niż ![]() tłuszczu. Wynik zapisz w postaci ułamka dziesiętnego
w zaokrągleniu do części tysięcznych. Zapisz obliczenia.
tłuszczu. Wynik zapisz w postaci ułamka dziesiętnego
w zaokrągleniu do części tysięcznych. Zapisz obliczenia.
Zadanie 4. (0-4)
Funkcja ![]() jest określona wzorem
jest określona wzorem
![]()
Oblicz współczynniki
Zadanie 5. (0-3)
Wykaż, że jeżeli ![]() oraz
oraz ![]() , to
, to ![]() .
.
Zadanie 6. (0-3)
Rozważamy wszystkie liczby naturalne, w których zapisie dziesiętnym nie powtarza się
jakakolwiek cyfra oraz dokładnie trzy cyfry są nieparzyste i dokładnie dwie cyfry są parzyste.
Oblicz, ile jest wszystkich takich liczb. Zapisz obliczenia.
Zadanie 7. (0-4)
Trzywyrazowy ciąg ![]() jest geometryczny i rosnący. Suma wyrazów tego ciągu jest
równa
jest geometryczny i rosnący. Suma wyrazów tego ciągu jest
równa ![]() . Liczby
. Liczby ![]() ,
, ![]() oraz
oraz ![]() są – odpowiednio – pierwszym, drugim oraz szóstym wyrazem ciągu arytmetycznego
są – odpowiednio – pierwszym, drugim oraz szóstym wyrazem ciągu arytmetycznego ![]() , określonego dla każdej liczby naturalnej
, określonego dla każdej liczby naturalnej ![]() .
.
Oblicz ![]() ,
, ![]() oraz
oraz ![]() . Zapisz obliczenia.
. Zapisz obliczenia.
Zadanie 8. (0-4)
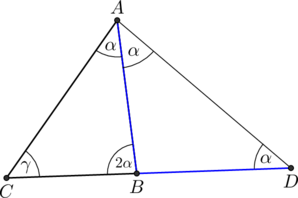
Dany jest trójkąt ![]() , który nie jest równoramienny. W tym trójkącie miara kąta
, który nie jest równoramienny. W tym trójkącie miara kąta ![]() jest
dwa razy większa od miary kąta
jest
dwa razy większa od miary kąta ![]() .
.
Wykaż, że długości boków tego trójkąta spełniają warunek
![]()
Zadanie 9. (0-4)
Dany jest kwadrat ![]() o boku długości
o boku długości ![]() . Punkt
. Punkt ![]() jest środkiem boku
jest środkiem boku ![]() . Przekątna
. Przekątna
![]() dzieli trójkąt
dzieli trójkąt ![]() na dwie figury:
na dwie figury: ![]() oraz
oraz ![]() (zobacz rysunek).
(zobacz rysunek).

Zadanie 10. (0-5)
Rozwiąż równanie
![]()
Zadanie 11. (0-5)
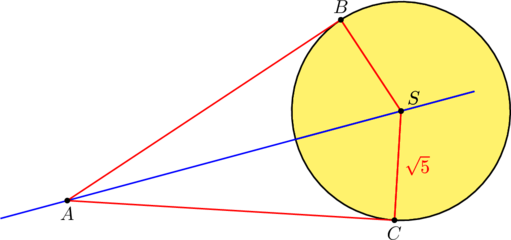
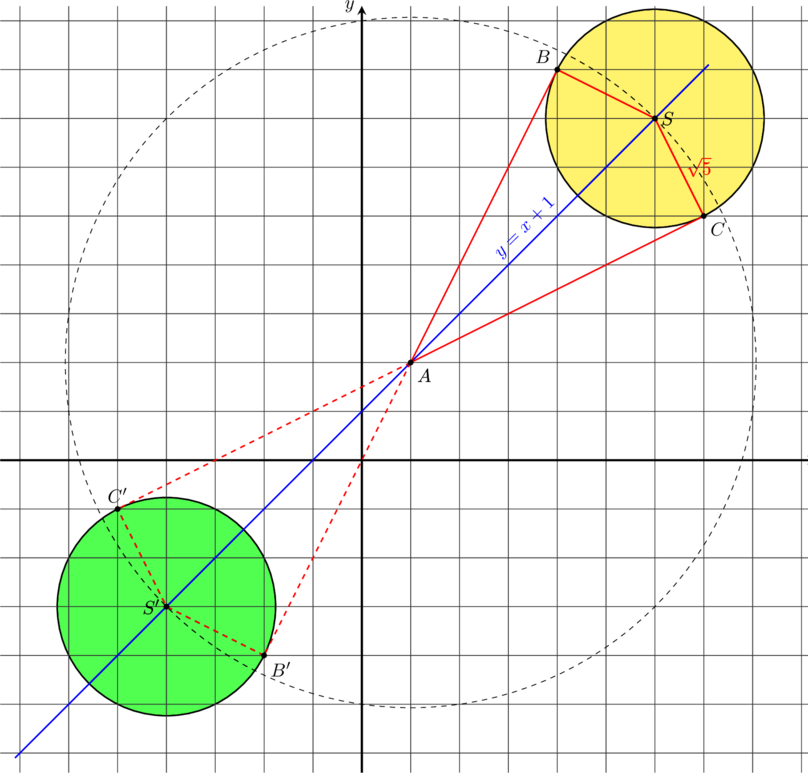
W kartezjańskim układzie współrzędnych ![]() środek
środek ![]() okręgu o promieniu
okręgu o promieniu ![]() leży na
prostej o równaniu
leży na
prostej o równaniu ![]() . Przez punkt
. Przez punkt ![]() , którego odległość od punktu
, którego odległość od punktu ![]() jest większa od
jest większa od ![]() , poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio –
, poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio – ![]() i
i ![]() . Pole czworokąta
. Pole czworokąta ![]() jest równe
jest równe ![]() .
.
Oblicz współrzędne punktu ![]() . Rozważ wszystkie przypadki. Zapisz obliczenia.
. Rozważ wszystkie przypadki. Zapisz obliczenia.
Zadanie 12. (0-6)
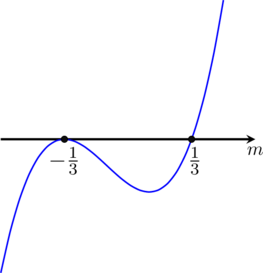
Wyznacz wszystkie wartości parametru ![]() , dla których równanie
, dla których równanie
![]()
![]()
Zadanie 13.
Rozważamy wszystkie graniastosłupy prawidłowe trójkątne o objętości ![]() , których
krawędź podstawy ma długość nie większą niż
, których
krawędź podstawy ma długość nie większą niż ![]() .
.
Zadanie 13.1 (0-2)
Wykaż, że pole ![]() powierzchni całkowitej graniastosłupa w zależności od długości
powierzchni całkowitej graniastosłupa w zależności od długości ![]() krawędzi podstawy graniastosłupa jest określone wzorem
krawędzi podstawy graniastosłupa jest określone wzorem
![]()
Zadanie 13.2 (0-4)
Pole ![]() powierzchni całkowitej graniastosłupa w zależności od długości
powierzchni całkowitej graniastosłupa w zależności od długości ![]() krawędzi podstawy graniastosłupa jest określone wzorem
krawędzi podstawy graniastosłupa jest określone wzorem
![]()
Wyznacz długość krawędzi podstawy tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole. Zapisz obliczenia.
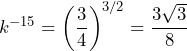 i stąd
i stąd![Rendered by QuickLaTeX.com \begin{eqnarray*} \lim\limits_{x\to 2^{-}}\frac{x^3-8}{(x-2)^2}&=&\lim\limits_{x\to 2^{-}}\frac{(x-2)(x^2+2x+4)}{(x-2)^2}=\nonumber\\ &=&\lim\limits_{x\to 2^{-}}\frac{x^2+2x+4}{x-2}=\left[\frac{4+4+4}{0^{-}}\right]=-\infty.\nonumber \end{eqnarray*}](https://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-5e704bda7024c4c37b57bde4922e833f_l3.png)