Zadanie 1. (0-6)
Punkt ![]() jest jednym z wierzchołków trójkąta równoramiennego
jest jednym z wierzchołków trójkąta równoramiennego ![]() , w którym
, w którym
![]() . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe ![]() . Bok
. Bok ![]() jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu ![]() . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka ![]() .
.
♦ matura – poziom rozszerzony, maj 2010.
Zadanie 2. (0-5)
Rysunek przedstawia fragment wykresu funkcji ![]() . Przeprowadzono prostą równoległą do osi
. Przeprowadzono prostą równoległą do osi ![]() , która przecięła wykres tej funkcji w punktach
, która przecięła wykres tej funkcji w punktach ![]() i
i ![]() . Niech
. Niech ![]() . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta ![]() jest większe lub równe 2.
jest większe lub równe 2.

♦ matura – poziom rozszerzony, maj 2010.
Zadanie 3. (0-6)
Zaznacz na płaszczyźnie zbiór
![]()
♦ matura – poziom rozszerzony, maj 2002.
Zadanie 4. (0-4)
W układzie współrzędnych są dane punkty: ![]() oraz
oraz ![]() . Wyznacz współrzędne
punktu
. Wyznacz współrzędne
punktu ![]() , leżącego na osi
, leżącego na osi ![]() , tak że kąt
, tak że kąt ![]() jest kątem prostym.
jest kątem prostym.
♦ matura próbna – poziom rozszerzony, styczeń 2003.
Zadanie 5. (0-4)
Wyznacz równanie okręgu opisanego na trójkącie, którego boki zawierają się w prostych o równaniach ![]() ,
, ![]() oraz
oraz ![]() .
.
♦ matura próbna ,,Operon” – poziom rozszerzony, listopad 2019.

![Rendered by QuickLaTeX.com \[A=\left(-\sqrt{\frac{1}{a}},\,a\right),\quad B=\left(\sqrt{\frac{1}{a}},\,a\right).\]](https://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-a7ba13c04e7def153e343f3ba2e943c9_l3.png)

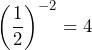 .
.


![Rendered by QuickLaTeX.com \[\left(x+\frac{5}{2}\right)^2+(y-0)^2=\left(\frac{\sqrt{185}}{2}\right)^2=\frac{185}{4}.\]](https://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-392ed879cbf75cd7ffdbc344689aef21_l3.png)
