Geometria - zadania na dowodzenie | Matematyczne nietuzinki ;)

Zadanie 1. (0-4)
Na bokach $BC$ i $CD$ równoległoboku $ABCD$ zbudowano kwadraty $CDEF$ i $BCGH$ (zobacz rysunek). Udowodnij, że $|AC| = |FG|$ .

Rendered by QuickLaTeX.com

♦ matura – poziom rozszerzony, maj 2010.

Zaznaczmy na rysunku interesujące nas odcinki i rozważmy taki dodatkowy punkt $X$ , aby czworokąt $CFXG$ był równoległobokiem.

Rendered by QuickLaTeX.com

Wtedy ten nowy równoległobok jest przystający do wyjściowego równoległoboku $ABCD$ . Odpowiednie przekątne też są jednakowe, a ponieważ $\angle BCD+\angle FCG=180^\circ$ , to przekątne $FG$ i $AC$ są właśnie jednakowej długości. To kończy dowód.

Zadanie 2. (0-4)
Trapez równoramienny $ABCD$ o podstawach $AB$ i $CD$ jest opisany na okręgu o promieniu $r$ . Wykaż, że $4r^2=|AB|\cdot |CD|$ .

♦ matura – poziom rozszerzony, maj 2013.

Wykonajmy stosowny rysunek. Zauważmy przy tym, że szkic wykorzystuje dodatkowe założenie, że $|AB|\geqslant |CD|$ . Należy mieć tego świadomość i w rozwiązaniu odpowiednio się do tego odnieść.

Rendered by QuickLaTeX.com

Z warunku opisywalności czworokąta na okręgu wiemy, że suma jego podstaw jest równa sumie długości ramion, czyli

$|AB|+|CD|=2|BC|,$

bo trapez jest równoramienny. Stąd $|BC|=\dfrac{|AB|+|CD|}{2}$ . Wykorzystajmy teraz twierdzenie pitagorasa dla trójkąta $BCE$ , gdzie punkt $E$ jest podstawą wysokości trapezu poprawodznej z wierzchołka $C$ . Wtedy, znów korzystając z równych długości ramion i symetrii całej figury, mamy $|BE|=\dfrac{|AB|-|CD|}{2}$ . Uwaga. Gdyby przyjąć, że to podstawa $|CD|$ jest dłuższa od podstawy $|AB|$ , to odpowiedni odcinek miałby długość $\dfrac{|CD|-|AB|}{2}$ , jednak nie wpływa to na dalsze obliczenia (gdyż kwadrat obu wyrażeń jest taki sam).

Z twierdzenia Pitagorasa mamy teraz $|BC|^2=(2r)^2+\left(\frac{|AB|-|CD|}{2}\right)^2$ , czyli

$4r^2=\left(\frac{|AB|+|CD|}{2}\right)^2-\left(\frac{|AB|-|CD|}{2}\right)^2=|AB|\cdot |CD|,$

co mieliśmy pokazać.

Zadanie 3. (0-4)
Trapez równoramienny, o obwodzie równym $20$ cm, jest opisany na okręgu. Wiedząc, że przekątna trapezu ma długość $\sqrt{41}$ cm, oblicz pole tego trapezu.

♦ matura próbna – poziom rozszerzony, maj 2003.

Przyjmijmy oznaczenia jak na rysunku; zakładamy (bez zmniejszenia ogólności rozważań), że $a\geqslant b$ . Rachunki będziemy przeprowadzać w centymetrach, co uwzględnimy formułując końcową odpowiedź.

Rendered by QuickLaTeX.com

Z warunku opisywalności czworokąta na okręgu i z tego, że trapez jest równoramienny wynika, że suma długości przeciwległych boków jest równa połowie obwodu: $a+b=2|BC|=10$ . Stąd $|BC|=5$ oraz $a+b=5$ .

Napiszmy twierdzenie Pitagorasa dla trójkątów $ACE$ i $BCE$ . Mamy

$h^2+|AE|^2=41\quad\text{oraz}\quad h^2+|BE|^2=25.$

Wiemy też, że $|AE|=\dfrac{a+b}{2}$ i $|BE|=\dfrac{a-b}{2}$ . Podstawiając to do wcześniejszych równości i odejmując je stronami, uzyskamy

$16=|AE|^2-|BE|^2=(|AE|-|BE|)(|AE|+|BE|)=ab.$

Mamy więc $a+b=10$ i $ab=16$ . Rozwiązując ten układ równań dostaniemy $b=10-a$ i dalej $a(10-a)=16$ , czyli $a^2-10a+16=0$ , a stąd $(a-8)(a-2)=0$ . To prowadzi nas do możliwych rozwiązań $(a,b)=(2,8)$ lub $(a,b)=(8,2)$ , jednak $a\geqslant b$ , czyli $a=8$ i $b=2$ .

Wówczas $|AE|=5$ i stąd $h^2+5^2=41$ , czyli $h^2=16$ , więc $h=4$ . To już prowadzi do odpowiedzi: szukane pole trapezu wynosi $P=\dfrac{a+b}{2}\cdot h=5\cdot 4=20$ cm $^{2}$ .

Zadanie 4. (0-3)
Dany jest trójkąt prostokątny o przyprostokątnych długości $a$ i $b$ , w którym kąt między środkową a wysokością wychodzącymi z wierzchołka kąta prostego ma miarę $\alpha$ . Wykaż, że $\text{tg}\alpha=\dfrac{|a^2-b^2|}{2ab}$ .

♦ matura próbna ,,Operon” – poziom rozszerzony, listopad 2019.

Rozważmy trójkąt prostokątny $ABC$ , w którym punkt $M$ jest środkiem przeciwprostokątnej $AB$ , zaś $H$ jest spodkiem wysokości opuszczonej z wierzchołka $C$ .

Rendered by QuickLaTeX.com

Oznaczmy $|CH|=h$ , $|AB|=c$ , $|BC|=a$ oraz $|CA|=b$ . Zauważmy, że porównując pole trójkąta $ABC$ mamy zależność $\dfrac{ab}{2}=\dfrac{ch}{2}$ , czyli $h=\dfrac{ab}{c}$ . Dodatkowo $|MC|=|MB|=\dfrac{c}{2}$ . Stąd

$\cos\alpha=\frac{h}{|MC|}=\frac{h}{c/2}=\frac{2ab}{c^2}=\frac{2ab}{a^2+b^2}.$

Ponieważ $\text{tg}\alpha=\dfrac{\sin\alpha}{\cos\alpha}$ , to mamy

(1) $\begin{eqnarray*} \text{tg}\alpha &=&\frac{\sqrt{1-\cos^2\alpha}}{\cos\alpha}=\frac{\sqrt{1-\frac{4a^2b^2}{(a^2+b^2)^2}}}{\frac{2ab}{a^2+b^2}}=\nonumber\\ &=&\frac{\sqrt{(a^2+b^2)^2-4a^2b^2}}{2ab}=\frac{\sqrt{(a^2-b^2)^2}}{2ab}=\frac{|a^2-b^2|}{2ab}.\nonumber \end{eqnarray*}$

To kończy dowód.

Zadanie 5. (0-2)
W trójkącie ostrokątnym $ABC$ wiadomo,że $\sin\angle BAC=\dfrac{4}{5}$ , a $\sin\angle ABC=\dfrac{2\sqrt{2}}{3}$ . Oblicz $\cos\angle ACB$ .

♦ matura próbna ,,Nowa Era” – poziom rozszerzony, styczeń 2018.

Oznaczmy odpowiednie kąty trójkąta przez $\alpha$ , $\beta$ i $\gamma$ . Ponieważ trójkąt jest ostrokątny, więc wartości wszystkich funkcji trygonometrycznych wskazanych kątów są wszystkie dodatnie. Stąd, jeżeli $\sin\alpha=\dfrac{4}{5}$ , to $\cos\alpha=\sqrt{1-\dfrac{4^2}{5^2}}=\dfrac{3}{5}$ . Podobnie, skoro $\sin\beta=\dfrac{2\sqrt{2}}{3}$ , to $\cos\beta=\sqrt{1-\dfrac{8}{9}}=\dfrac{1}{3}$ .

Rendered by QuickLaTeX.com

Mamy oczywiście $\gamma=180^\circ-(\alpha+\beta)$ , czyli

$\cos\gamma=-\cos(\alpha+\beta)=\sin\alpha\cdot\sin\beta-\cos\alpha\cdot\cos\beta.$

Podstawiając wyliczone wartości, otrzymujemy $\cos\gamma=\dfrac{4}{5}\cdot\dfrac{2\sqrt{2}}{3}-\dfrac{3}{5}\cdot\dfrac{1}{3}=\dfrac{8\sqrt{2}-3}{15}$ .

Zadanie 6. (0-3)
W czworokącie $ABCD$ dane są: $|AC|=5$ , $\angle BAD=\angle BCD=90^\circ$ , $\sin\angle ABC=\dfrac{\sqrt{5}}{3}$ . Oblicz długość przekątnej $BD$ tego czworokąta.

♦ matura próbna ,,Nowa Era” – poziom rozszerzony, styczeń 2018.

Dany czworokąt można wpisać okrąg (bo suma jego przeciwległych kątów wynosi $180^\circ$ ), przy czym przekątna $BD$ jest średnicą tego okręgu.

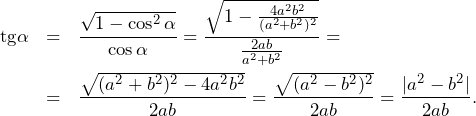
Rendered by QuickLaTeX.com

Okrąg ten jest jednocześnie okręgiem opisanym na trójkącie $ABC$ , więc jego promień $R$ , z twierdzenia sinusów, spełnia równość

$R=\dfrac{|AC|}{\sin\beta}=\dfrac{5}{\frac{\sqrt{5}}{3}}=3\sqrt{5}.$

Stąd odpowiedź: $|BD|=2R=6\sqrt{5}$ .

Kategoria: Geometria – zadania na dowodzenie

Geometria i zadania na dowodzenie – przykłady z rozwiązaniami