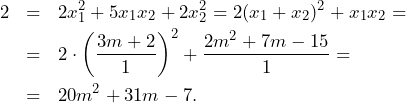Poniżej prezentujemy rozwiązania wszystkich zadań maturalnych z matematyki dla poziomu rozszerzonego, z którymi abiturienci mierzyli się 7. maja 2020 r. Zadania pochodzą z arkusza opublikowanego w serwisie Centralnej Komisji Egzaminacyjnej.
Zadanie 1. (0-1)
Wielomian ![]() określony wzorem
określony wzorem ![]()
A. jest podzielny przez ![]() i z dzielenia przez
i z dzielenia przez ![]() daje resztę równą
daje resztę równą ![]()
B. jest podzielny przez ![]() i z dzielenia przez
i z dzielenia przez ![]() daje resztę równą
daje resztę równą ![]()
C. jest podzielny przez ![]() i jest podzieleny przez
i jest podzieleny przez ![]()
D. nie jest podzielny ani przez ![]() , ani przez
, ani przez ![]()
Zadanie 2. (0-1)
Ciąg ![]() jest określony wzorem
jest określony wzorem ![]() dla każdej liczby naturalnej
dla każdej liczby naturalnej ![]() . Granica tego ciągu jest równa
. Granica tego ciągu jest równa
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 3. (0-1)
Mamy dwie urny. W pierwszej są ![]() kule białe i
kule białe i ![]() kul czarnych, w drugiej jest jedna kula biała i
kul czarnych, w drugiej jest jedna kula biała i ![]() kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z jednym oczkiem, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest
równe
kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z jednym oczkiem, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest
równe
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 4. (0-1)
Po przekształceniu wyrażenia algebraicznego ![]() do postaci
do postaci ![]() współczynnik
współczynnik ![]() jest równy
jest równy
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 5. (0-2)
W trójkącie ![]() bok
bok ![]() jest
jest ![]() razy dłuższy od boku
razy dłuższy od boku ![]() , a długość boku
, a długość boku ![]() stanowi
stanowi ![]() długości boku
długości boku ![]() . Oblicz cosinus najmniejszego kąta trójkąta
. Oblicz cosinus najmniejszego kąta trójkąta ![]() .
.
W kratki poniżej wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.

Zadanie 6. (0-3)
Wyznacz wszystkie wartości parametru ![]() , dla których równanie
, dla których równanie
![]()
Zadanie 7. (0-3)
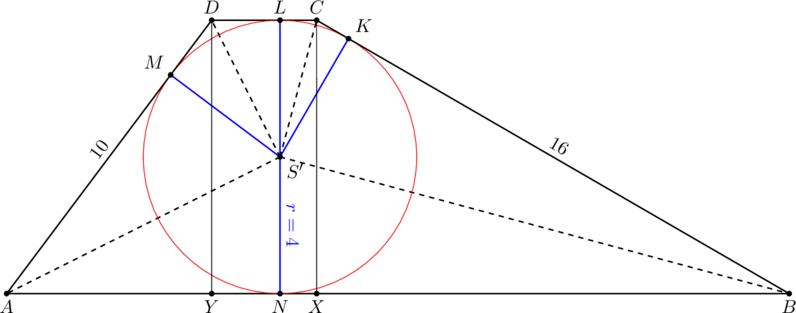
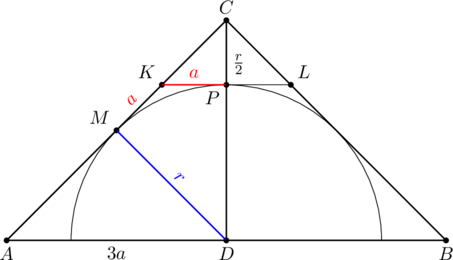
Dany jest trójkąt równoramienny ![]() , w którym
, w którym ![]() , a punkt
, a punkt ![]() jest środkiem
podstawy
jest środkiem
podstawy ![]() . Okrąg o środku
. Okrąg o środku ![]() jest styczny do prostej
jest styczny do prostej ![]() w punkcie
w punkcie ![]() . Punkt
. Punkt ![]() leży na boku
leży na boku ![]() , punkt
, punkt ![]() leży na boku
leży na boku ![]() , odcinek
, odcinek ![]() jest styczny do rozważanego okręgu oraz
jest styczny do rozważanego okręgu oraz ![]() (zobacz rysunek).
(zobacz rysunek).
Zadanie 8. (0-3)
Liczby dodatnie ![]() i
i ![]() spełniają równość
spełniają równość ![]() . Wykaż, że
. Wykaż, że ![]() .
.
Zadanie 9. (0-4)
Rozwiąż równanie ![]() dla
dla ![]() .
.
Zadanie 10. (0-5)
W trzywyrazowym ciągu geometrycznym ![]() spełniona jest równość
spełniona jest równość ![]() . Wyrazy
. Wyrazy ![]() ,
, ![]() ,
, ![]() są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz
są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz ![]() .
.
Zadanie 11. (0-4)
Dane jest równanie kwadratowe ![]() z niewiadomą
z niewiadomą ![]() . Wyznacz
wszystkie wartości parametru
. Wyznacz
wszystkie wartości parametru ![]() , dla których różne rozwiązania
, dla których różne rozwiązania ![]() i
i ![]() tego równania istnieją i spełniają warunek
tego równania istnieją i spełniają warunek
![]()
Zadanie 12. (0-5)
Prosta o równaniu ![]() przecina okrąg o równaniu
przecina okrąg o równaniu ![]() w punktach
w punktach ![]() i
i ![]() . Punkt
. Punkt ![]() jest środkiem cięciwy
jest środkiem cięciwy ![]() . Wyznacz równanie obrazu tego okręgu w jednokładności o środku
. Wyznacz równanie obrazu tego okręgu w jednokładności o środku ![]() i skali
i skali ![]() .
.
Zadanie 13. (0-4)
Oblicz, ile jest wszystkich siedmiocyfrowych liczb naturalnych, w których zapisie dziesiętnym
występują dokładnie trzy cyfry ![]() i dokładnie dwie cyfry
i dokładnie dwie cyfry ![]() .
.
Zadanie 14. (0-6)
Podstawą ostrosłupa czworokątnego ![]() jest trapez
jest trapez ![]()
![]() . Ramiona tego trapezu mają długości
. Ramiona tego trapezu mają długości ![]()
![]() , a miara kąta
, a miara kąta ![]() jest równa
jest równa ![]() . Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt
. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt ![]() , taki, że
, taki, że ![]() . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Zadanie 15. (0-7)
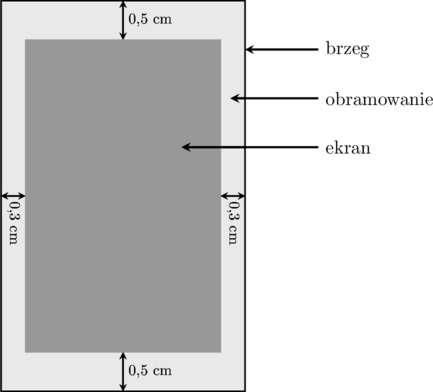
Należy zaprojektować wymiary prostokątnego ekranu smartfona, tak aby odległości tego
ekranu od krótszych brzegów smartfona były równe ![]() cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe
cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe ![]() cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię
cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię ![]() cm
cm![]() . Wyznacz takie wymiary ekranu
smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.
. Wyznacz takie wymiary ekranu
smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.
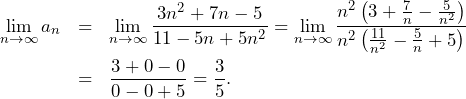
![Rendered by QuickLaTeX.com \[\cos \beta=\frac{9+\frac{144}{25}-1}{\frac{72}{5}}=\frac{344}{360}=\frac{43}{45}\approx 0,\!95555.\]](https://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-1cbcc355e3a3b1d3974ca9aebe4c9305_l3.png)
![Rendered by QuickLaTeX.com \[\frac{|AM|}{|MC|}=\frac{6-2-\frac{4}{3}}{\frac{4}{3}+2}=\frac{4}{5},\]](https://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-ed3561f5cb0ba20f1f70888ad0b680e5_l3.png)