Poniżej prezentujemy rozwiązania wszystkich zadań maturalnych z matematyki dla poziomu rozszerzonego, z którymi abiturienci mierzyli się 12. maja 2023 r. Zadania pochodzą z arkusza opublikowanego w serwisie Centralnej Komisji Egzaminacyjnej.
Zadanie 1. (0-1)
Granica ![]() jest równa
jest równa
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 2. (0-1)
Dane są wektory ![]() oraz
oraz ![]() . Długość wektora
. Długość wektora ![]() jest równa
jest równa
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 3. (0-1)
Punkty ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() leżą na okręgu o środku
leżą na okręgu o środku ![]() . Miara kąta
. Miara kąta ![]() jest równa
jest równa ![]() , a miara kąta
, a miara kąta ![]() jest równa
jest równa ![]() (zobacz rysunek).
(zobacz rysunek).

A.
B.
C.
D.
Zadanie 4. (0-1)
Dany jest zbiór trzynastu liczb ![]() , z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch
liczb, których iloczyn jest liczbą parzystą, jest
, z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch
liczb, których iloczyn jest liczbą parzystą, jest
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 5. (0-2)
Wielomian ![]() ma dokładnie jeden pierwiastek rzeczywisty.
Oblicz ten pierwiastek.
ma dokładnie jeden pierwiastek rzeczywisty.
Oblicz ten pierwiastek.
W poniższe kratki wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.

Zadanie 6. (0-3)
Liczby rzeczywiste ![]() oraz
oraz ![]() spełniają jednocześnie równanie
spełniają jednocześnie równanie ![]() i nierówność
i nierówność
![]() . Wykaż, że
. Wykaż, że ![]() oraz
oraz ![]() .
.
Zadanie 7. (0-3)
Dany jest trójkąt prostokątny ![]() , w którym
, w którym ![]() oraz
oraz ![]() . Punkty
. Punkty ![]() i
i ![]() leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – ![]() i
i ![]() tak, że
tak, że ![]() (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek ![]() przecina wysokość
przecina wysokość ![]() tego trójkąta w punkcie
tego trójkąta w punkcie ![]() , a ponadto
, a ponadto ![]() .
.

Wykaż, że ![]() .
.
Zadanie 8. (0-3)
W pojemniku jest siedem kul: pięć kul białych i dwie kule czarne. Z tego pojemnika losujemy jednocześnie dwie kule bez zwracania. Następnie – z kul pozostałych w pojemniku – losujemy jeszcze jedną kulę. Oblicz prawdopodobieństwo wylosowania kuli czarnej w drugim losowaniu.
Zadanie 9. (0-3)
Funkcja ![]() jest określona wzorem
jest określona wzorem ![]() dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej ![]() . Punkt
. Punkt ![]() należy do wykresu funkcji
należy do wykresu funkcji ![]() . Oblicz
. Oblicz ![]() oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji ![]() w punkcie
w punkcie ![]() .
.
Zadanie 10. (0-4)
Rozwiąż nierówność
![]()
Zadanie 11. (0-4)
Określamy kwadraty ![]() następująco:
następująco:
• ![]() jest kwadratem o boku długości
jest kwadratem o boku długości ![]()
• ![]() jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu ![]() i dzieli ten bok w stosunku
i dzieli ten bok w stosunku ![]()
• ![]() jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu ![]() i dzieli ten bok w stosunku
i dzieli ten bok w stosunku ![]()
i ogólnie, dla każdej liczby naturalnej ![]()
• ![]() jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu ![]() i dzieli ten bok w stosunku
i dzieli ten bok w stosunku ![]() .
.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg
geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.

Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Zadanie 12. (0-4)
Rozwiąż równanie ![]() w przedziale
w przedziale ![]() .
.
Zadanie 13. (0-4)
Czworokąt ![]() , w którym
, w którym ![]() i
i ![]() , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna ![]() tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem ![]() kąt o mierze
kąt o mierze ![]() , natomiast z bokiem
, natomiast z bokiem ![]() – kąt ostry, którego sinus jest równy
– kąt ostry, którego sinus jest równy ![]() . Oblicz obwód czworokąta
. Oblicz obwód czworokąta ![]() .
.
Zadanie 14. (0-4)
Dany jest sześcian ![]() o krawędzi długości
o krawędzi długości ![]() . Punkt
. Punkt ![]() jest punktem przecięcia
przekątnych
jest punktem przecięcia
przekątnych ![]() i
i ![]() ściany bocznej
ściany bocznej ![]() (zobacz rysunek).
(zobacz rysunek).

Zadanie 15. (0-5)
Wyznacz wszystkie wartości parametru ![]() , dla których równanie
, dla których równanie
![]()
Zadanie 16. (0-7)
Rozważamy trójkąty ![]() , w których
, w których ![]() ,
, ![]() , gdzie
, gdzie ![]() , a wierzchołek
, a wierzchołek ![]() leży na prostej o równaniu
leży na prostej o równaniu ![]() . Na boku
. Na boku ![]() tego trójkąta leży punkt
tego trójkąta leży punkt
![]() .
.
a) Wykaż, że dla ![]() pole
pole ![]() trójkąta
trójkąta ![]() , jako funkcja zmiennej
, jako funkcja zmiennej ![]() , wyraża się wzorem
, wyraża się wzorem
![]()
b) Oblicz tę wartość ![]() , dla której funkcja
, dla której funkcja ![]() osiąga wartość najmniejszą. Wyznacz równanie prostej
osiąga wartość najmniejszą. Wyznacz równanie prostej ![]() , przy której funkcja
, przy której funkcja ![]() osiąga tę najmniejszą wartość.
osiąga tę najmniejszą wartość.
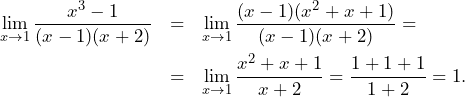



![Rendered by QuickLaTeX.com \[p_1=\frac{\binom{5}{2}}{\binom{7}{2}}=\frac{10}{21},\quad p_2=\frac{\binom{5}{1}\binom{2}{1}}{\binom{7}{2}}=\frac{10}{21},\quad p_3=\frac{\binom{2}{2}}{\binom{7}{2}}=\frac{1}{21}.\]](https://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6da02ff4cda534b47943cc3970f0bb96_l3.png)

![Rendered by QuickLaTeX.com \[S=\frac{r_1}{1-q}=\frac{4a}{1-\frac{\sqrt{10}}{4}}=\frac{16}{4-\sqrt{10}}a=\frac{8(4+\sqrt{10})}{3}a.\]](https://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-0a94334c98c6aec62d0d85b35b011758_l3.png)


