2019 | Matematyczne nietuzinki ;)

Poniżej prezentujemy rozwiązania wszystkich zadań maturalnych z matematyki dla poziomu rozszerzonego, z którymi abiturienci mierzyli się 9. maja 2019 r. Zadania pochodzą z arkusza opublikowanego w serwisie Centralnej Komisji Egzaminacyjnej.

Zadanie 1. (0-1)
Dla dowolnych liczb $x>0$ , $x\neq 1$ , $y>0$ , $y\neq 1$ wartość wyrażenia $\left(\log_{\frac{1}{x}}y\right)\cdot \left(\log_{\frac{1}{y}}x\right)$ jest równa
   A. $x\cdot y$
   B. $\frac{1}{x\cdot y}$
   C. $-1$
   D. $1$

Z własności logarytmów, przy podanych założeniach mamy

(1) $\begin{eqnarray*} \left(\log_{\frac{1}{x}}y\right)\cdot \left(\log_{\frac{1}{y}}x\right)&=&\frac{1}{\log_y\frac{1}{x}}\cdot\frac{1}{\log_x\frac{1}{y}}=\nonumber\\[0.25cm] &=&\left(-\frac{1}{\log_yx}\right)\cdot\left(-\frac{1}{\log_xy}\right)=\nonumber\\[0.25cm] &=&\frac{1}{\log_yx}\cdot\log_yx=1.\nonumber \end{eqnarray*}$

Zatem poprawną jest odpowiedź D.

Zadanie 2. (0-1)
Liczba $\cos^2105^\circ-\sin^2105^\circ$ jest równa jest równa
   A. $-\frac{\sqrt{3}}{2}$
   B. $-\frac{1}{2}$
   C. $\frac{1}{2}$
   D. $\frac{\sqrt{3}}{2}$

Ze wzoru na cosinus podwojonego argumentu mamy

(2) $\begin{eqnarray*} \cos^2105^\circ-\sin^2105^\circ&=&\cos(2\cdot 105^\circ)=\cos 210^\circ=\nonumber\\ &=&\cos(30^\circ+180^\circ)=-\cos30^\circ=-\frac{\sqrt{3}}{2}.\nonumber \end{eqnarray*}$

Poprawną odpowiedzią jest A.

Zadanie 3. (0-1)
Na rysunku przedstawiono fragment wykresu funkcji $y=f(x),$ który jest złożony z dwóch półprostych $AD$ i $CE$ oraz dwóch odcinków $AB$ i $BC$ , gdzie $A=(-1,0),$ $B=(1,2),$ $C=(3,0),$ $D=(-4,3)$ , $E=(6,3)$ .

Rendered by QuickLaTeX.com

Wzór funkcji $f$ to:
   A. $f(x)=|x+1|+|x-1|$
   B. $f(x)=||x-1|-2|$
   C. $f(x)=||x-1|+2|$
   D. $f(x)=|x-1|+2$

Z opisu wykresu funkcji $f(x)$ wynika w szczególności, że $f(0)=1$ . Podstawiając argument $x=0$ do podanych czterech propozycji odpowiedzi, widzimy, że kolejne wartości są równe: $f_A(0)=2$ , $f_B(0)=1$ , $f_C(0)=3$ oraz $f_D(0)=3$ . Zatem poprawną odpowiedzią jest B.

Zadanie 4. (0-1)
Zdarzenia losowe $A$ i $B$ zawarte w $\Omega$ są takie, że prawdopodobieństwo $P(B')$ zdarzenia $B'$ , przeciwnego do zdarzenia $B$ , jest równe $\frac{1}{4}.$ Ponadto prawdopodobieństwo warunkowe $P(A|B)=\frac{1}{5}.$ Wynika stąd, że
   A. $P(A\cap B)=\frac{1}{20}$
   B. $P(A\cap B)=\frac{4}{15}$
   C. $P(A\cap B)=\frac{3}{20}$
   D. $P(A\cap B)=\frac{4}{5}$

Mamy $P(A|B)=\frac{P(A\cap B)}{P(B)}$ , czyli

$P(A\cap B)=P(A|B)\cdot P(B)=P(A|B)\cdot (1-P(B'))=\frac{1}{5}\cdot\frac{3}{4}=\frac{3}{20}.$

Odpowiedź C.

Zadanie 5. (0-2)
Obliczyć granicę

$\lim\limits_{n\to\infty}\left(\frac{9n^3+11n^2}{7n^3+5n^2+3n+1}-\frac{n^2}{3n^2+1}\right).$

Wpisz w poniższe kratki – od lewej do prawej – trzy kolejne cyfry po przecinku rozwinięcia dziesiętnego otrzymanego wyniku.

Rendered by QuickLaTeX.com

Wyłączając przed nawias, z liczników i mianowników obu ułamków, dominujący czynnik (czyli odpowiednio $n^3$ i $n^2$ , otrzymamy

(3) $\begin{eqnarray*} &{}&\lim\limits_{n\to\infty}\left(\frac{9n^3+11n^2}{7n^3+5n^2+3n+1}-\frac{n^2}{3n^2+1}\right)=\nonumber\\ &=&\lim\limits_{n\to\infty}\left(\frac{n^3\big(9+\frac{11}{n}\big)}{n^3\big(7+\frac{5}{n}+\frac{3}{n^2}+\frac{1}{n^3}\big)}-\frac{n^2}{n^2\big(3+\frac{1}{n^2}\big)}\right)=\nonumber\\ &=&\frac{9}{7}-\frac{1}{3}=\frac{27}{21}-\frac{7}{21}=\frac{20}{21}\approx 0,\!95238095\ldots\nonumber \end{eqnarray*}$

To oznacza, że w kratki należało wpisać cyfry $9$ , $5$ i $2$ .

Zadanie 6. (0-3)
Rozważamy wszystkie liczby naturalne pięciocyfrowe zapisane przy użyciu cyfr 1, 3, 5, 7, 9, bez powtarzania jakiejkolwiek cyfry. Oblicz sumę wszystkich takich liczb.

Wszystkich permutacji pięciu podanych cyfry jest $5!=120$ . Każda z nich odpowiada jednemu składnikowi sumy, którą mamy obliczyć. W dokładnie $4!=\frac{5!}{5}=24$ różnych składnikach cyfra $1$ będzie stanowiła cyfrę jedności; w tylu samo składnikach cyfrą jedności będzie $3$ itd. dla każdej z ustalonych pięciu cyfr. Podobnie sytuacja wygląda dla kolejnych rzędów (tzn. dla cyfr dziesiątek, setek, itd.) Ponieważ wkład tych cyfr do szukanej sumy $S$ wynosi

$24\cdot(1+3+5+7+9)=24\cdot 25=600$

dla każdego dostępnego rzędu wielkości, więc

$S=600\cdot (1+10+100+1000+10000)=600\cdot 11111=6666600.$

Zadanie 7. (0-2)
Punkt $P=(10,2429)$ leży na paraboli o równaniu $y=2x^2+x+2219$ Prosta o równaniu kierunkowym $y=ax+b$ jest styczna do tej paraboli w punkcie $P$ . Oblicz współczynnik $b$ .

Niech $f(x)=2x^2+x+2219$ będzie daną funkcją kwadratową. Współczynnik $a$ prostej stycznej jest wartością pochodnej funkcji $f(x)$ dla argumentu $x=10$ (zgodnego ze współrzędną odciętą punktu $P$ ). Mamy $f'(x)=4x+1$ , stąd $a=f'(10)=4\cdot 10+1=41$ . Styczna przechodzi przez punkt $P$ , więc $2429=41\cdot 10+b$ , a stąd $b=2429-410=2019$ .

Zadanie 8. (0-3)
Udowodnij, że dla dowolnych dodatnich liczb rzeczywistych $x$ i $y$ , takich że $x<y,$ i dowolnej dodatniej liczby rzeczywistej $a$ , prawdziwa jest nierówność $\dfrac{x+a}{y+a}+\dfrac{y}{x}>2.$

Zauważmy, że dla $y>x$ i $a>0$ prawdziwa jest nierówność

$(x-y)^2+a(y-x)>0.$

Wynika z niej, że $x(x+a)+y(y+a)>2xy+2ax$ . Dzieląc ostatnią nierówność obustronnie przez liczbę dodatnią $x(y+a)$ otrzymamy

$\frac{x+a}{y+a}+\frac{y}{x}>2,$

to kończy dowód.

Zadanie 9. (0-3)
Dany jest trójkąt równoramienny $ABC$ , w którym $|AC|=|BC|.$ Na ramieniu $AC$ tego trójkąta wybrano punkt $M$ ( $M\neq A$ i $M\neq C$ ), a na ramieniu $BC$ wybrano punkt $N$ , w taki sposób, że $|AM|=|CN|.$ Przez punkty $M$ i $N$ poprowadzono proste prostopadłe do podstawy $AB$ tego trójkąta, które wyznaczają na niej punkty $S$ i $T$ . Udowodnij, że $|ST|=\frac{1}{2}|AB|.$

Rendered by QuickLaTeX.com

Sytuacja wygląda jak na rysunku. Poprowadźmy odcinek $CP$ , będący wysokością trójkąta $ABC$ wychodzącą z wierzchołka $C$ oraz odcinek $NK$ , gdzie $K$ jest rzutem prostokątnym punktu $N$ na wysokość $CP$ . Wówczas odcinki $NK$ i $AB$ są równoległe (bo są prostopadłe do wspólnej wysokości $CP$ ). Ponieważ trójkąt $ABC$ jest równoramienny, to z równoległości tej mamy równości kątów: $\angle BAC=\angle CNK$ oraz $\angle AMS=\angle KCN$ (wysokość poprowadzona na podstawę w trójkącie równoramiennym jest jednocześnie dwusieczną kąta). Z treści zadania mamy jeszcze $|AM|=|CN|$ , zatem trójkąty $\triangle\, AMS$ i $\triangle\, NCK$ są przystające (cecha kąt-bok-kąt). W szczególności mamy $|AS|=|KN|=|PT|$ . To już oznacza, że

$\frac{1}{2}|AB|=|AP|=|AS|+|SP|=|PT|+|SP|=|ST|,$

a to kończy dowód.

Zadanie 10. (0-4)
Punkt $D$ leży na boku $AB$ trójkąta $ABC$ oraz $|AC|=16,$ $|AD|=6,$ $|CD|=14,$ $|BC|=|BD|.$ Oblicz obwód trójkąta $ABC$ .

Rendered by QuickLaTeX.com

Niech $x=|BC|=|BD|$ . Wykorzystamy dwukrotnie twierdzenie kosinusów. Najpierw dla trójkąta $ADC,$ aby wyznaczyć kosinus kąta $\beta=\angle ADC.$ Mamy $16^2=6^2+14^2-2\cdot 6\cdot 14\cos\beta$ , czyli

$\cos\beta=\frac{36+196-256}{12\cdot 14}=-\frac{1}{7}.$

Zatem $\cos\angle CDB=\cos(180^\circ-\beta)=-\cos\beta=\frac{1}{7}$ . Stąd – stosując drugi raz twierdzenie kosinusów – w trójkącie równoramiennym $BCD$ mamy

$x^2=14^2+x^2-2\cdot 14x\cos\angle CDB,$

czyli $2\cdot 14x\cdot\frac{1}{7}=196$ , a zatem $x=49$ . To oznacza, że szukany obwód trójkąta $ABC$ wynosi $|AB|+|BC|+|CA|=(6+49)+49+16=120.$

Zadanie 11. (0-6)
Dane są okręgi o równaniach $x^2+y^2-12x-8y+43=0$ i $x^2+y^2-2ax+4y+a^2-77=0$ . Wyznacz wszystkie wartości parametru $a,$ dla których te okręgi mają dokładnie jeden punkt wspólny. Rozważ wszystkie przypadki.

Dane równania można przekształcić do postaci $(x-6)^2+(y-4)^2=3^2$ oraz $(x-a)^2+(y+2)^2=9^2$ . To oznacza, że pierwszy okrąg — oznaczmy go przez $\omega_1$ , ma środek w punkcie $O_1=(6,4)$ i promieniu $r_1=3$ . Drugi okrąg zaś – nazwijmy go $\omega_2$ – ma środek w punkcie $O_2=(a,-2)$ i promień $r_2=9$ .

Rendered by QuickLaTeX.com

Dane okręgi mogą być styczne zewnętrznie lub wewnętrznie. Ponieważ środki okręgu $\omega_2$ leżą na prostej $y=-2$ , to styczność wewnętrzna może się zdarzyć jedynie dla $a=4$ – wówczas bowiem środki obu okręgów będą możliwie najbliżej siebie i $|O_1O_2|=6=r_2-r_1$ .

Obliczymy teraz te wartości $a$ , dla których okręgi są styczne zewnętrznie. Musi być wtedy spełniony warunek $|O_1O_2|=r_1+r_2$ , czyli

$\sqrt{(6-a)^2+(4-(-2))^2}=12\qquad\Longleftrightarrow\qquad (6-a)^2=108.$

Stąd $a=6\sqrt{3}+6$ lub $a=-6\sqrt{3}+6$ . Ostatecznie mamy więc trzy możliwe rozwiązania: $a=6$ , $a=6-6\sqrt{3}$ i $a=6+6\sqrt{3}$ .

Zadanie 12. (0-6)
Trzywyrazowy ciąg $(a,b,c)$ o wyrazach dodatnich jest arytmetyczny, natomiast ciąg $\left(\dfrac{1}{a},\dfrac{2}{3b},\,\dfrac{1}{2a+2b+c}\right)$ jest geometryczny. Oblicz iloraz ciągu geometrycznego.

Z warunku na ciąg arytmetyczny mamy $2b=a+c$ , natomiast z warunku na ciąg geometryczny jest $\left(\dfrac{2}{3b}\right)^2=\dfrac{1}{a}\cdot\dfrac{1}{2a+2b+c}$ . Wyznaczając $b$ z pierwszej zależności i wstawiając do drugiej, otrzymujemy

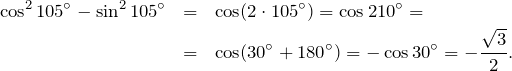
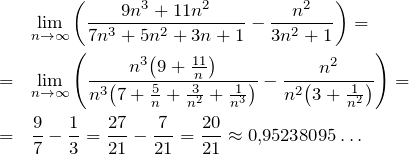
$\left(\frac{2}{3\cdot\frac{a+c}{2}}\right)^2=\frac{1}{a}\cdot\frac{1}{2a+a+c+c}.$

Porządkując wyrazy, mamy $\frac{16}{9(a+c)^2}=\frac{1}{a(3a+2c)}$ , czyli $9(a+c)^2=16a(3a+2c)$ . Podstawiając zmienną pomocniczą $t=\frac{a}{c}$ , po obustronnym podzieleniu ostatniego równania przez $c^2$ , dostaniemy

$9(t+1)^2=16t(3t+2)\quad\Leftrightarrow\quad $39t^2+14t-9=0.$

Obliczamy wyróżnik $\Delta=14^2+4\cdot 39\cdot 9=1600$ , więc $t_1=\frac{-14-40}{78}<0$ oraz $t_2=\frac{-14+40}{78}=\frac{1}{3}$ . Pierwsze rozwiązanie odrzucamy, bo $t=\frac{a}{c}>0$ dla $a,c>0$ .

Obliczamy iloraz ciągu geometrycznego. Wynosi on

$q=\frac{2}{3b}:\frac{1}{a}=\frac{2a}{3b}=\frac{4a}{3(a+c)}=\frac{4t}{3(t+1)}=\frac{4/3}{1+3}=\frac{1}{3}.$

Zadanie 13. (0-6)
Wielomian określony wzorem $W(x)=2x^3+(m^3+2)x^2-11x-2(2m+1)$ jest podzielny przez dwumian $(x-2)$ oraz przy dzieleniu przez dwumian $(x+1)$ daje resztę $6.$ Oblicz $m$ i dla wyznaczonej wartości $m$ rozwiąż nierówność $W(x)\leqslant 0$ .

Na podstawie twierdzenia Bézouta mamy $W(2)=0$ oraz $W(-1)=6$ . Stąd $2\cdot 2^3+(m^3+2)\cdot 2^2-11\cdot 2-2(2m+1)=0$ , czyli $4m^3-4m=0$ . To prowadzi do $4m(m-1)(m+1)=0$ , więc $m\in\{-1,\,0,\,1\}.$ Wystarcz teraz zobaczyć, która z tych trzech możliwości spełnia drugi warunek: $W(-1)=6$ . Ponieważ $W(-1)=m^3-4m+9$ , to widzimy, że musi być $m=1.$

Interesuje nas więc wielomian $W(x)=2x^3+3x^2-11x-6$ . Wykorzystując ponownie informację o pierwiastku $W(2)=0$ , po wykonaniu dzielenia $W(x):(x-2)$ otrzymujemy zależność

$W(x)=(x-2)(2x^2+7x+3).$

Możemy obliczyć pierwiastki drugiego czynnika: $\Delta=49-24=25$ , czyli $x_1=\frac{-7-5}{4}=-3$ oraz $x_2=\frac{-7+5}{4}=-\frac{1}{2}$ . Zatem

$W(x)=(x-2)(x+3)(2x+1).$

Rendered by QuickLaTeX.com

Z pomocniczego wykresu odczytujemy rozwiązanie nierówności $W(x)\leqslant 0$ . Tworzy je suma przedziałów $(-\infty,\,-3]\cup \left[-\frac{1}{2},2\right]$ .

Zadanie 14. (0-4)
Rozwiąż równanie $(\cos x)\left[\sin\left(x-\dfrac{\pi}{3}\right)+\sin\left(x+\dfrac{\pi}{3}\right)\right]=\dfrac{1}{2}\sin x.$

Wykorzystamy wzór na sinus sumy argumentów: $\sin(x+y)=\sin x\cos y+\cos x\sin y$ . Stąd mamy

(4) $\begin{eqnarray*} &{}&\sin\left(x-\dfrac{\pi}{3}\right)+\sin\left(x+\dfrac{\pi}{3}\right)=\nonumber\\[0.25cm] &=&\sin x\cos\frac{\pi}{3}-\cos x\sin\frac{\pi}{3}+\sin x\cos\frac{\pi}{3}+\cos x\sin\frac{\pi}{3}=\sin x. \end{eqnarray*}$

Równanie przyjmuje więc postać $2\cos x\sin x=\sin x$ , czyli $\sin x(2\cos x-1)=0$ . To prowadzi do alternatywy: $\sin x=0$ lub $\cos x=\frac{1}{2}$ . Stąd odpowiedź

$x=k\pi\quad\text{lub}\quad x=\frac{\pi}{3}+2k\pi\quad\text{lub}\quad x=-\frac{\pi}{3}+2k\pi,$

gdzie $k$ jest liczbą całkowitą.

Zadanie 15. (0-7)
Rozważmy wszystkie graniastosłupy prawidłowe trójkątne o objętości $V=2.$ Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.

Niech $x>0$ będzie długością krawędzi podstawy, zaś $h>0$ wysokością (i jednocześnie długością krawędzi bocznej) w rozważanych graniastosłupach. Mamy $V=\frac{\sqrt{3}}{4}x^2h=2$ , a stąd $h=\frac{8}{\sqrt{3}}\cdot\frac{1}{x^2}$ .

Niech $S=f(x)$ będzie polem powierzchni całkowitej naszego graniastosłupa. Wówczas na $S$ składają się pola dwóch podstaw (trójkątów równobocznych o krawędzi $x$ ) oraz pola trzech ścian bocznych (prostokątów $x\times h$ ). Stąd, wykorzystując zależność na $V$ , mamy

$f(x)=S=2\cdot\frac{\sqrt{3}}{4}x^2+3xh=\frac{\sqrt{3}}{2}x^2+\frac{8\sqrt{3}}{x}.$

Naszym celem jest wyznaczenie minimum funkcji $f(x)$ dla $x>0$ . Można wykorzystać rachunek różniczkowy, lub posłużyć się nierównością pomiędzy średnią geometryczną i średnią arytmetyczną dla trzech liczb dodatnich: $\sqrt[3]{abc}\leqslant\dfrac{a+b+c}{3}$ dla dowolnych $a,b,c>0$ ; równość zachodzi jedynie dla $a=b=c$ .

Przyjmijmy w powyższej nierówności $a=b=\frac{8}{x}$ oraz $c=x^2$ . Wtedy $4=\sqrt[3]{\frac{8}{x}\cdot\frac{8}{x}\cdot x^2}\leqslant \frac{\frac{8}{x}+\frac{8}{x}+x^2}{3}$ , czyli

$x^2+\frac{16}{x}\geqslant 12$

i równość zachodzi wyłącznie dla $x^2=\frac{8}{x}$ , a więc dla $x^3=8$ , skąd $x=2$ .

Zauważmy, że nierówność powyższa pozwala nam napisać

(5) $\begin{eqnarray*} f(x)&=&\frac{\sqrt{3}}{2}x^2+\frac{8\sqrt{3}}{x}=\frac{\sqrt{3}}{2}\left(x^2+\frac{16}{x}\right)\geqslant\nonumber\\[0.25cm] &\geqslant&\frac{\sqrt{3}}{2}\cdot 12=6\sqrt{3}.\nonumber \end{eqnarray*}$

Oznacza to, że szukany graniastosłup ma krawędzie długości $x=2$ , $h=\frac{8}{\sqrt{3}}\cdot\frac{1}{2^2}=\frac{2\sqrt{3}}{3}$ , a jego objętość wynosi $6\sqrt{3}$ .

Tag: 2019

Matura rozszerzona z matematyki (maj 2019) – rozwiązania