Poniżej prezentujemy rozwiązania wszystkich zadań maturalnych z matematyki dla poziomu rozszerzonego, z którymi abiturienci mierzyli się 12. maja 2023 r. Zadania pochodzą z arkusza opublikowanego w serwisie Centralnej Komisji Egzaminacyjnej.
Zadanie 1. (0-1)
Granica ![]() jest równa
jest równa
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 2. (0-1)
Dane są wektory ![]() oraz
oraz ![]() . Długość wektora
. Długość wektora ![]() jest równa
jest równa
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 3. (0-1)
Punkty ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() leżą na okręgu o środku
leżą na okręgu o środku ![]() . Miara kąta
. Miara kąta ![]() jest równa
jest równa ![]() , a miara kąta
, a miara kąta ![]() jest równa
jest równa ![]() (zobacz rysunek).
(zobacz rysunek).
![\begin{tikzpicture}[scale=1.3] \draw (0,0) circle (2cm); \coordinate (A) at (275:2); \coordinate (B) at (345:2); \coordinate (C) at (55:2); \coordinate (D) at (125:2); \coordinate (E) at (200:2); \foreach \x/\w in {A/275,B/345,C/55,D/125,E/200} \draw[fill=black] (\x) circle (1pt) node at (\w:2.28) {$\x$}; \draw[fill=black] (0,0) circle (1pt) node[below right] {$S$}; \draw[thick] (A)--(B)--(C)--(D)--(E)--cycle; \draw (B)--(D)--(A); \draw[thin,shift={(C)}] (180:0.7) arc (180:290:0.7) node[scale=0.75] at (235:0.4) {$110^\circ$}; \draw[thin,shift={(D)}] (290:1.3) arc (290:325:1.3) node[scale=0.8] at (307:1) {$35^\circ$}; \draw[thin,shift={(E)}] (327:0.6) arc (327:432:0.6); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6db04fd5e1281457204b7a8f4133fa3e_l3.png)
A.
B.
C.
D.
Zadanie 4. (0-1)
Dany jest zbiór trzynastu liczb ![]() , z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch
liczb, których iloczyn jest liczbą parzystą, jest
, z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch
liczb, których iloczyn jest liczbą parzystą, jest
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 5. (0-2)
Wielomian ![]() ma dokładnie jeden pierwiastek rzeczywisty.
Oblicz ten pierwiastek.
ma dokładnie jeden pierwiastek rzeczywisty.
Oblicz ten pierwiastek.
W poniższe kratki wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.
![\begin{tikzpicture}[yscale=1.5,scale=0.8] \draw[very thick] (0,0) grid (3,1); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-c5183acb72d252f5924056c98e521912_l3.png)
Zadanie 6. (0-3)
Liczby rzeczywiste ![]() oraz
oraz ![]() spełniają jednocześnie równanie
spełniają jednocześnie równanie ![]() i nierówność
i nierówność
![]() . Wykaż, że
. Wykaż, że ![]() oraz
oraz ![]() .
.
Zadanie 7. (0-3)
Dany jest trójkąt prostokątny ![]() , w którym
, w którym ![]() oraz
oraz ![]() . Punkty
. Punkty ![]() i
i ![]() leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – ![]() i
i ![]() tak, że
tak, że ![]() (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek ![]() przecina wysokość
przecina wysokość ![]() tego trójkąta w punkcie
tego trójkąta w punkcie ![]() , a ponadto
, a ponadto ![]() .
.
![\begin{tikzpicture}[scale=1.3] \coordinate (A) at (0,4); \coordinate (B) at (0,0); \coordinate (C) at (6.9282,0); \coordinate (K) at (0,1); \coordinate (L) at (1,0); \coordinate (D) at ($(A)!(B)!(C)$); \coordinate (N) at (intersection of B--D and K--L); \foreach \x/\r in {A/{above},B/{below left},C/{below},D/{above right},K/{left},L/{below},N/{right}} \draw[fill=black] (\x) circle (0.8pt) node[\r] {$\x$}; \draw (B)--(D); \draw[thin] (A)--(D) node[midway,above right] {$2$}; \draw[thin] (B)--(L) node[midway,below] {$1$}; \draw[thin] (B)--(K) node[midway,left] {$1$}; \draw[thick] (C)--(B)--(A)--cycle; \draw (K)--(L); \draw[thin,shift={(A)}] (270:0.7) arc (270:330:0.7) node at (300:0.5) {$60^\circ$}; \draw[thin,shift={(D)}] (150:0.5) arc (150:240:0.5) node[scale=2] at (195:0.3) {$\cdot$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-2f0b674b5ab00c414b440467e1a35151_l3.png)
Wykaż, że ![]() .
.
Zadanie 8. (0-3)
W pojemniku jest siedem kul: pięć kul białych i dwie kule czarne. Z tego pojemnika losujemy jednocześnie dwie kule bez zwracania. Następnie – z kul pozostałych w pojemniku – losujemy jeszcze jedną kulę. Oblicz prawdopodobieństwo wylosowania kuli czarnej w drugim losowaniu.
Zadanie 9. (0-3)
Funkcja ![]() jest określona wzorem
jest określona wzorem ![]() dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej ![]() . Punkt
. Punkt ![]() należy do wykresu funkcji
należy do wykresu funkcji ![]() . Oblicz
. Oblicz ![]() oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji ![]() w punkcie
w punkcie ![]() .
.
Zadanie 10. (0-4)
Rozwiąż nierówność
![]()
Zadanie 11. (0-4)
Określamy kwadraty ![]() następująco:
następująco:
• ![]() jest kwadratem o boku długości
jest kwadratem o boku długości ![]()
• ![]() jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu ![]() i dzieli ten bok w stosunku
i dzieli ten bok w stosunku ![]()
• ![]() jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu ![]() i dzieli ten bok w stosunku
i dzieli ten bok w stosunku ![]()
i ogólnie, dla każdej liczby naturalnej ![]()
• ![]() jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu ![]() i dzieli ten bok w stosunku
i dzieli ten bok w stosunku ![]() .
.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg
geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
![\begin{tikzpicture}[scale=1.3] \coordinate (A) at (0,0); \coordinate (B) at (4,0); \coordinate (C) at (4,4); \coordinate (D) at (0,4); \node[below] at (2,0) {$a$}; \node[left] at (0,2) {$a$}; \foreach \x in {1,...,10} { \draw (A)--(B)--(C)--(D)--cycle; \coordinate (A1) at ($(A)!0.25!(B)$); \coordinate (B1) at ($(B)!0.25!(C)$); \coordinate (C1) at ($(C)!0.25!(D)$); \coordinate (D1) at ($(D)!0.25!(A)$); \draw (A1)--(B1)--(C1)--(D1)--cycle; \coordinate (A) at ($(A1)!0.25!(B1)$); \coordinate (B) at ($(B1)!0.25!(C1)$); \coordinate (C) at ($(C1)!0.25!(D1)$); \coordinate (D) at ($(D1)!0.25!(A1)$); } \draw[thick] (0,0)--(4,0)--(4,4)--(0,4)--cycle; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-56c042f0f396eae990eb7cabe9ca71ab_l3.png)
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Zadanie 12. (0-4)
Rozwiąż równanie ![]() w przedziale
w przedziale ![]() .
.
Zadanie 13. (0-4)
Czworokąt ![]() , w którym
, w którym ![]() i
i ![]() , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna ![]() tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem ![]() kąt o mierze
kąt o mierze ![]() , natomiast z bokiem
, natomiast z bokiem ![]() – kąt ostry, którego sinus jest równy
– kąt ostry, którego sinus jest równy ![]() . Oblicz obwód czworokąta
. Oblicz obwód czworokąta ![]() .
.
Zadanie 14. (0-4)
Dany jest sześcian ![]() o krawędzi długości
o krawędzi długości ![]() . Punkt
. Punkt ![]() jest punktem przecięcia
przekątnych
jest punktem przecięcia
przekątnych ![]() i
i ![]() ściany bocznej
ściany bocznej ![]() (zobacz rysunek).
(zobacz rysunek).
![\begin{tikzpicture}[scale=0.9] \coordinate (A) at (0,0); \coordinate (B) at (5,0); \coordinate (C) at (7,2); \coordinate (D) at (2,2); \coordinate (E) at (0,5); \coordinate (F) at (5,5); \coordinate (G) at (7,7); \coordinate (H) at (2,7); \coordinate (S) at (1,3.5); \draw[thick] (A)--(B)--(C)--(G)--(H)--(E)--cycle (F)--(G) (E)--(F)--(B); \draw[thick,dashed] (A)--(D)--(H) (D)--(C); \draw[dotted,thick,black!75] (A)--(H) (E)--(D); \node[below] at (2.5,0) {$6$}; \foreach \x/\r in {A/{below left},B/{below right},C/right,D/{below right},E/left,F/right,G/{above right},H/above,S/left} \draw[fill=black] (\x) circle (1pt) node[\r] {$\x$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-7971549f258193790573f1f2e81614a8_l3.png)
Zadanie 15. (0-5)
Wyznacz wszystkie wartości parametru ![]() , dla których równanie
, dla których równanie
![]()
Zadanie 16. (0-7)
Rozważamy trójkąty ![]() , w których
, w których ![]() ,
, ![]() , gdzie
, gdzie ![]() , a wierzchołek
, a wierzchołek ![]() leży na prostej o równaniu
leży na prostej o równaniu ![]() . Na boku
. Na boku ![]() tego trójkąta leży punkt
tego trójkąta leży punkt
![]() .
.
a) Wykaż, że dla ![]() pole
pole ![]() trójkąta
trójkąta ![]() , jako funkcja zmiennej
, jako funkcja zmiennej ![]() , wyraża się wzorem
, wyraża się wzorem
![]()
b) Oblicz tę wartość ![]() , dla której funkcja
, dla której funkcja ![]() osiąga wartość najmniejszą. Wyznacz równanie prostej
osiąga wartość najmniejszą. Wyznacz równanie prostej ![]() , przy której funkcja
, przy której funkcja ![]() osiąga tę najmniejszą wartość.
osiąga tę najmniejszą wartość.
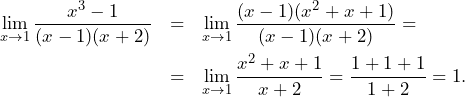
![\begin{tikzpicture}[scale=1.3] \draw (0,0) circle (2cm); \coordinate (A) at (275:2); \coordinate (B) at (345:2); \coordinate (C) at (55:2); \coordinate (D) at (125:2); \coordinate (E) at (200:2); \foreach \x/\w in {A/275,B/345,C/55,D/125,E/200} \draw[fill=black] (\x) circle (1pt) node at (\w:2.28) {$\x$}; \draw[fill=black] (0,0) circle (1pt) node[left] {$S$}; \draw[thick] (A)--(B)--(C)--(D)--(E)--cycle; \draw (B)--(D)--(A); \draw[thin,shift={(C)}] (180:0.7) arc (180:290:0.7) node[scale=0.75] at (235:0.4) {$110^\circ$}; \draw[thin,shift={(D)}] (290:1.3) arc (290:325:1.3) node[scale=0.8] at (307:1) {$35^\circ$}; \draw[thin,shift={(E)}] (327:0.6) arc (327:432:0.6); \draw[blue] (A)--(0,0)--(B) (B)--(0,0)--(D); \draw[thin,shift={(E)}] (327:0.6) arc (327:432:0.6); \draw[thin,red] (275:0.5) arc (275:345:0.5) node[red,scale=0.8] at (310:0.35) {$70^\circ$}; \draw[thin,red] (345:0.4) arc (345:485:0.4) node[red,scale=0.7] at (55:0.23) {$140^\circ$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-a92854f5ea19a24185ce2f283a863a94_l3.png)
![\begin{tikzpicture}[scale=1.3] \coordinate (A) at (0,4); \coordinate (B) at (0,0); \coordinate (C) at (6.9282,0); \coordinate (K) at (0,1); \coordinate (L) at (1,0); \coordinate (D) at ($(A)!(B)!(C)$); \coordinate (N) at (intersection of B--D and K--L); \foreach \x/\r in {A/{above},B/{below left},C/{below},D/{above right},K/{left},L/{below},N/{right}} \draw[fill=black] (\x) circle (0.8pt) node[\r] {$\x$}; \draw (B)--(D); \draw[thin] (A)--(D) node[midway,above right] {$2$}; \draw[thin] (B)--(K) node[midway,left] {$1$}; \draw[thick] (C)--(B)--(A)--cycle; \draw (K)--(L); \draw[thin,shift={(A)}] (270:0.7) arc (270:330:0.7) node at (300:0.5) {$60^\circ$}; \draw[thin,shift={(D)}] (150:0.5) arc (150:240:0.5) node[scale=2] at (195:0.3) {$\cdot$}; \coordinate (P) at ($(B)!(N)!(L)$); \draw[fill=blue!20] (B)--(N)--(P)--cycle; \draw[red] (N)--(P) node[below] {$P$}; \draw[thin,red] (N)--(P) node[right,midway,scale=0.7] {$x$}; \draw[thin,red] (L)--(P) node[above,midway,scale=0.7] {$x$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-886f944440d9d8ed184e6c23f8af632c_l3.png)
![\begin{tikzpicture}[scale=1.3,sibling distance=25mm, level distance=20mm] \node {$(5b+2c)$} child {node {$(3b+2c)$} child {node {$b$}} child {node {$c$}}} child {node {$(4b+1c)$} child {node {}} child {node {$b$}}} child {node {$(5b)$} child {node {}} child {node {$c$}} }; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-622ec857167a83c62d00ae6828efca43_l3.png)
![\[p_1=\frac{\binom{5}{2}}{\binom{7}{2}}=\frac{10}{21},\quad p_2=\frac{\binom{5}{1}\binom{2}{1}}{\binom{7}{2}}=\frac{10}{21},\quad p_3=\frac{\binom{2}{2}}{\binom{7}{2}}=\frac{1}{21}.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6da02ff4cda534b47943cc3970f0bb96_l3.png)
![\begin{tikzpicture} \draw[very thick, ->] (-3.5,0)--(3.9,0) node[below] {$x$}; \foreach \x in {-2,0,3} \draw (\x,0)--(\x,-0.07) node[below] {$\x$}; \draw[thin,blue] (-3.2,0.4)--(-2.2,0.4)--(-2,0.05)--(-1.8,0.4)--(2.8,0.4)--(3,0.05)--(3.2,0.4)--(3.8,0.4); \node[above,red,scale=1.3] at (-2.7,0.3) {$1^\circ$}; \node[above,red,scale=1.3] at (0.5,0.3) {$2^\circ$}; \node[above,red,scale=1.3] at (3.5,0.3) {$3^\circ$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-35b3bffe486210721d3bfb6ba9070a3a_l3.png)
![\[S=\frac{r_1}{1-q}=\frac{4a}{1-\frac{\sqrt{10}}{4}}=\frac{16}{4-\sqrt{10}}a=\frac{8(4+\sqrt{10})}{3}a.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-0a94334c98c6aec62d0d85b35b011758_l3.png)
![\begin{tikzpicture}[scale=0.65] \coordinate (A) at (-7.32,4.94); \coordinate (B) at (6.46,6.56); \coordinate (C) at (7.97,2.85); \coordinate (D) at (5.97,-1.73); \coordinate (O) at (4.3,2.9); \foreach \x/\w in {A/left,B/above,C/right,D/below} \draw[fill=black] (\x) circle (1pt) node[\w] {$\x$}; \draw[blue] (A)--(C); \draw[thin] (B)--(C) node[midway,right] {$4$}; \draw[thin] (D)--(C) node[midway,right] {$5$}; \draw[thin] (B)--(A) node[midway,above] {$a$}; \draw[thin] (D)--(A) node[midway,below] {$b$}; \draw[thin,shift={(A)}] (352:3) arc (352:366.5:3) node at (360:2.3) {$\alpha$}; \draw[thin,shift={(C)}] (472:1.4) arc (472:532:1.4) node at (501:0.9) {$60^\circ$}; \draw[thick] (A)--(B)--(C)--(D)--cycle; \draw[red] (O) circle (3.387cm); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-743b65edb950204a509aa81d6e247292_l3.png)
![\begin{tikzpicture}[scale=0.9] \coordinate (A) at (0,0); \coordinate (B) at (5,0); \coordinate (C) at (7,2); \coordinate (D) at (2,2); \coordinate (E) at (0,5); \coordinate (F) at (5,5); \coordinate (G) at (7,7); \coordinate (H) at (2,7); \coordinate (S) at (1,3.5); \coordinate (K) at ($(B)!(S)!(H)$); \draw[fill=yellow!30] (A)--(B)--(G)--(H)--cycle; \draw[fill=blue!30] (S)--(B)--(H)--cycle; \draw[red,thick] (S)--(K) node[below right,midway] {$d$}; \draw[thick] (A)--(B)--(C)--(G)--(H)--(E)--cycle (F)--(G) (E)--(F)--(B); \draw[thick,dashed] (A)--(D)--(H) (D)--(C); \draw[dotted,thick,black!75] (A)--(H) (E)--(D); \node[below] at (2.5,0) {$6$}; \foreach \x/\r in {A/{below left},B/{below right},C/right,D/{below right},E/left,F/right,G/{above right},H/above,S/left} \draw[fill=black] (\x) circle (1pt) node[\r] {$\x$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-4e76ba7ad62cd979b06e96275aef6685_l3.png)
![\begin{tikzpicture}[scale=1] \coordinate (A) at (0,0); \coordinate (B) at (6,0); \coordinate (D) at (3,2); \coordinate (C) at (-3,6); \draw[fill=yellow!40] (A)--(B)--(C)--cycle; \draw[black!70] (-6.4,-1.2) grid (6.3,8.3); \draw[very thick,->] (-6.4,0)--(6.3,0) node[below] {$x$}; \draw[very thick,->] (0,-1.2)--(0,8.3) node[left] {$y$}; \draw[thick,blue,dashed] (-4.3,8.6)--(1,-2) node[below,sloped,midway] {$y=-2x$}; \draw[very thick,brown,dashed] (4,-1.2)--(4,8.3); \foreach \x in {A,B,D,C} \draw[fill=black] (\x) circle (1.7pt) node[below left] {$\x$}; \node[below left] at (4,0) {$4$}; \node[above] at (B) {$(m,0)$}; \node[above] at (D) {$(3,2)$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-e9f93e7a2397370367fb95608694c52d_l3.png)
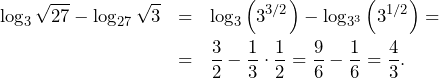
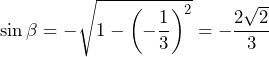 . Mamy też
. Mamy też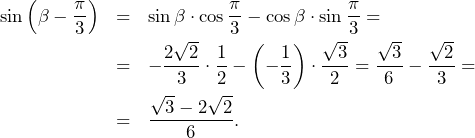
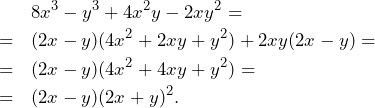
![\begin{tikzpicture}[scale=0.9] \coordinate[label=below left:$A$] (A) at (200:3); \coordinate[label=below right:$B$] (B) at (340:3); \coordinate[label=above:$C$] (C) at (2,4); \coordinate[label=above:$D$] (D) at (-1.2,4); \coordinate[label=right:$P$] (P) at (intersection of A--C and B--D); \draw (C)--(D) node[above,midway] {$a$}; \draw (A)--(B) node[below,midway] {$a+2$}; \draw[thick] (A)--(C); \draw[thick] (B)--(D); \draw[thick] (A)--(B)--(C)--(D)--cycle; \draw[thin,blue,shift={(P)}] (46:0.6) arc (46:127:0.6) node at (88:0.4) {$\alpha$}; \draw[thin,blue,shift={(P)}] (226:0.6) arc (226:307:0.6) node at (268:0.4) {$\alpha$}; \node at (0.35,3.4) {$R$}; \node at (0.2,0.2) {$R+3$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-5dac939cc3c74eeb464f01438fa2b051_l3.png)
![\begin{tikzpicture}[scale=1.2,yscale=1] \draw[thin,fill=red!20] (-1,0) rectangle (0,0.4); \draw[red!20,thin,fill=red!20] (3,0) rectangle (3.9,0.4); \draw (3,0)--(3,0.4)--(3.9,0.4) ; \draw[thick,blue,domain=-1.7:3.3, smooth, variable=\x,yscale=0.2] plot ({\x},{(\x+1)*(\x+0)*(\x-3)}); \draw[very thick,->] (-1.8,0)--(4,0) node[below] {$x$}; \foreach \x/\w in {-1/{-1},0/{-\frac{1}{2}},3/3} { \draw (\x,0)--(\x,-0.06) node[below] {$\w$}; \draw[fill=black] (\x,0) circle (2pt);} \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-a971ee5d2cd14b5e06868d8ce48b2612_l3.png)
![\begin{tikzpicture}[scale=1.5] \draw[fill=blue!20,blue!20] (0,3.5)--(2,0)--(3,4.9); \draw[thick,dashed] (0,0)--(2,0)--(3,1.4)--(1,1.4)--cycle (1,1.4)--(1,4.9); \draw[thick] (0,0)--(2,0)--(3,1.4); \draw[thick,shift={(0,3.5)}] (0,0)--(2,0)--(3,1.4)--(1,1.4)--cycle; \draw[thick] (0,0)--(0,3.5) (2,0)--(2,3.5) (3,1.4)--(3,4.9); \draw[blue,thick] (0,3.5)--(2,0)--(3,4.9); \foreach \x/\y/\g/\w in {0/0/{below left}/D,2/0/{below right}/A,3/1.4/right/B,1/1.4/left/C, 0/3.5/{left}/H,2/3.5/{below right}/E,3/4.9/above/F,1/4.9/above/G } \node[\g] at (\x,\y) {$\w$}; \draw[thick,blue,shift={(2,0)}] (77:0.7) arc (77:120.5:0.7) node[black] at (99:0.55) {$\alpha$}; \node[left] at (0,1.75) {$h$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-ce47164bc74c45da52972417695ac07d_l3.png)
![\begin{tikzpicture}[scale=1.5] \draw (0,0)--(1,-4) node[left,midway] {$\sqrt{a^2+h^2}$}; \draw (3,0)--(1,-4) node[right,midway] {$\sqrt{b^2+h^2}$}; \draw (0,0)--(3,0) node[above,midway] {$\sqrt{a^2+b^2}$}; \draw[blue,thick,fill=blue!20] (0,0)--(3,0)--(1,-4)--cycle; \foreach \x/\y/\g/\w in {0/0/{above left}/H,3/0/{above right}/F,1/-4/below/A} \node[\g] at (\x,\y) {$\w$}; \draw[thick,blue,shift={(1,-4)}] (64:0.6) arc (64:105:0.6) node[black] at (84:0.4) {$\alpha$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-cbe0ef1ac00f092b63a39ff167ba5121_l3.png)
![\begin{tikzpicture}[scale=0.5] \draw[black!30] (-10.5,-9.5) grid (10.5,9.5); \draw[ultra thick,->] (-10.5,0)--(10.5,0) node[below] {$x$}; \draw[very thick,->] (0,-9.5)--(0,9.5) node[left] {$y$}; \coordinate[label=above:$A$] (A) at (-3,2); \coordinate[label=below right:$C$] (C) at (4,3); \coordinate[label=below right:$B_1$] (B1) at (9,8); \coordinate[label=left:$B_2$] (B2) at (-1,-2); \draw[blue] (-8,-9)--(10.5,9.5) node[below,sloped,near start] {$y=x-1$}; \draw[fill=black] (A) circle (0.09cm); \draw[fill=black] (C) circle (0.09cm); \draw[fill=black] (B1) circle (0.09cm); \draw[fill=black] (B2) circle (0.09cm); \draw[red,thick] (A)--(B1)--(C)--cycle; \draw[green!50!black,thick] (A)--(B2)--(C)--cycle; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-cb804ffffc8d9f294cfe3e78e0d8690b_l3.png)
![\begin{tikzpicture}[scale=1.4] \draw[thick](0,0)--(2,0)--(1,3)--cycle; \draw[thick,blue] (1,3)--(1,0); \node[left,blue] at (1,1.2) {$h$}; \node[below] at (1,0) {$a$}; \draw (0,0)--(1,3) node[left,midway] {$b$}; \draw (2,0)--(1,3) node[right,midway] {$b$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6567a63e847aa0c476b4e9175606affb_l3.png)
![\begin{tikzpicture}[scale=1.5,rotate=4] \coordinate[label=below:$A$] (A) at (0,0); \coordinate[label=right:$B$] (B) at (2,1); \coordinate[label=left:$C$] (C) at (-0.7,1.5); \coordinate[label=above:$D$] (D) at (0.7,4); \coordinate[label=right:$K$] (K) at ($(B)!0.3!(D)$); \coordinate[label=above right:$P$] (P) at ($0.333*(A)+0.333*(B)+0.333*(C)$); \draw[thick] (C)--(A)--(B) (A)--(D)--(B) (D)--(C); \draw[thick,dashed] (B)--(C); \foreach \p in {A,B,C,D,K,P} \draw[fill=black] (\p) circle (0.8pt); \node[scale=0.65,blue] at ($(K)+(208:0.4)$) {$2\alpha$}; \draw[blue] (K)--(A); \draw[blue,dashed] (K)--(C); \draw (B)--(A) node[below,midway] {$a$}; \draw (C)--(A) node[left,midway] {$a$}; \draw[thick,red] (D)--(P); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-faa7c325eaeaab50161ec661069ffd82_l3.png)
![\begin{tikzpicture} \draw[thick] (0,0)--(2,3)--(4,0)--cycle; \draw[thick,blue] (0,0)--(2,3)--(4,0); \node[above left] at (1,1.5) {$x$}; \node[below] at (1,0) {$\frac{a}{2}$}; \node[below left] at (0,0) {$C$}; \node[below right] at (4,0) {$A$}; \node[above] at (2,3) {$K$}; \draw[red] (2,3)--(2,0); \node[scale=0.8] at ($(2,3)+(252:0.4)$) {$\alpha$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-d309d4406520e9882ebef060a92ed7d8_l3.png)
![\begin{tikzpicture} \draw[thick] (0,0)--(2,5)--(4,0)--cycle; \node[above left] at (1,2.5) {$b$}; \node[below] at (1,0) {$\frac{a}{2}$}; \node[below left] at (0,0) {$A$}; \node[below right] at (4,0) {$B$}; \node[above] at (2,5) {$D$}; \draw[red] (2,5)--(2,0) node[right,midway] {$h$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-66d74b3405165f8e453a20ca56ade731_l3.png)
![\[H^2=b^2-\left(\frac{2}{3}\cdot \frac{\sqrt{3}}{2}a\right)^2=\frac{a^2\sin^2\alpha}{4\sin^2\alpha-1}-\frac{a^2}{9}=\frac{5\sin^2\alpha+1}{9\left(4\sin^2\alpha-1\right)}a^2.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-4cc4ff572ee0e22db0cc47a47ab8b129_l3.png)
![\[V=\frac{1}{3}\cdot\frac{\sqrt{3}}{4}a^2\cdot H=\frac{\sqrt{15\sin^2\alpha+3}}{36\sqrt{4\sin^2\alpha-1}}\,a^3.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-f6fdd5ab525a07e129b62ba464cc9d14_l3.png)
![\begin{tikzpicture} \coordinate[label=above:$C$] (C) at (0,0); \coordinate[label=below:$A$] (A) at (210:4); \coordinate[label=below:$A'$] (Ap) at (330:4); \coordinate[label=above left:$B$] (B) at (270:1.5); \draw[red] (B)--(270:2) node[right,midway] {$1$}; \draw[thick] (A)--(B)--(C)--cycle; \draw[thick,dashed,blue] (B)--(Ap)--(C); \draw (A)--(C) node[above left,midway] {$8$}; \node[right] at (0,-0.8) {$3$}; \node[scale=0.6,below] at (220:0.3) {$60^\circ$}; \draw[thin,red] (A)--(Ap); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-b82a78f56a9f0a8a3c1213063968bd03_l3.png)
![\begin{tikzpicture}[scale=0.9] \coordinate[label=below left:$A$] (A) at (0,0); \coordinate[label=below right:$B$] (B) at (3,0); \coordinate[label=above left:$A_1$] (A1) at (0,3); \coordinate[label=below right:$B_1$] (B1) at (3,3); \coordinate[label=below:$D$] (D) at (1.5,1); \coordinate[label=below right:$C$] (C) at (4.5,1); \coordinate[label=above left:$D_1$] (D1) at (1.5,4); \coordinate[label=above right:$C_1$] (C1) at (4.5,4); \coordinate[label=below left:$K$] (K) at (intersection of B--D1 and A1--C); \draw[thick] (A)--(B)--(B1)--(A1)--cycle (A1)--(B1)--(C1)--(D1)--cycle (B)--(C)--(C1); \draw[thick,dashed] (A)--(D)--(C) (D)--(D1); \draw[very thick, red] (D1)--(B) (A1)--(C); \foreach \p in {A,B,C,D,A1,B1,C1,D1,K} \draw[fill=black] (\p) circle (1.5pt); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-eea773a34a0e4ddb25bb4570c724ced7_l3.png)
![\begin{tikzpicture}[scale=2.5] \coordinate[label=below left:$A_1$] (A1) at (0,0); \coordinate[label=below right:$B$] (B) at (1.414,0); \coordinate[label=above right:$C$] (C) at (1.414,1); \coordinate[label=above left:$D_1$] (D1) at (0,1); \coordinate[label=below:$K$] (K) at (intersection of B--D1 and A1--C); \foreach \p in {A1,B,C,D1,K} \draw[fill=black] (\p) circle (0.4pt); \draw[thick] (A1)--(B)--(C)--(D1)--cycle; \draw[thick,red] (A1)--(C) (B)--(D1); \node[below] at (0.71,0) {$a\sqrt{2}$}; \node[left] at (0,0.5) {$a$}; \node[right,red] at (0.77,0.5) {$\alpha$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-fa5881053139903f01fa39bd016ce867_l3.png)
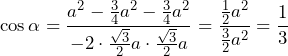 . To kończy rozwiązanie.
. To kończy rozwiązanie.
![\begin{tikzpicture}[scale=1.3] \coordinate[label=below left:$A$] (A) at (0,0); \coordinate[label=below right:$B$] (B) at (3,0); \coordinate[label=above left:$A_1$] (A1) at (0,2); \coordinate[label=below right:$B_1$] (B1) at (3,2); \coordinate[label=below:$D$] (D) at (1.5,1); \coordinate[label=below right:$C$] (C) at (4.5,1); \coordinate[label=above left:$D_1$] (D1) at (1.5,3); \coordinate[label=right:$C_1$] (C1) at (4.5,3); \coordinate[label=above:$P$] (P) at ($(D1)!0.6!(C1)$); \coordinate[label=below right:$Q$] (Q) at ($(B1)!0.6!(C1)$); \coordinate[label=left:$V$] (V) at ($(P)!0.5!(Q)$); \coordinate[label=below left:$T$] (T) at ($(B)!0.5!(D)$); \coordinate[label=left:$W$] (W) at (intersection of C--C1 and T--V); \draw[red,thick,fill=red!10] (B)--(Q)--(P)--(D)--cycle; \draw[thick] (A)--(B)--(B1)--(A1)--cycle (A1)--(B1)--(C1)--(D1)--cycle (B)--(C)--(C1); \draw[thick,dashed] (A)--(D)--(C) (D)--(D1); \node[above] at (B1) {$B_1$}; \node[below left] at (V) {$V$}; \draw[thick,blue] (C)--(T)--($(P)!0.5!(Q)$) (V)--(W)--(C1) (V)--(C1); \foreach \p in {A,B,C,D,A1,B1,C1,D1,P,Q,T,V,W} \draw[fill=black] (\p) circle (1.1pt); \node[scale=0.8,blue] at ($(T)+(30:0.42)$) {$60^\circ$}; \draw (A)--(B) node[below,midway] {$a$}; \draw (C)--(B) node[below right,midway] {$a$}; \draw (C)--(C1) node[right,midway] {$\frac{a}{2}$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-b5e4e85655deff24bc679d05d30ff4ea_l3.png)
![\[S=\frac{|BD|+|PQ|}{2}\cdot|TV|=\frac{a\sqrt{2}+\frac{a(\sqrt{6}-1)}{\sqrt{3}}}{2}\cdot \frac{a\sqrt{3}}{3}=\frac{a^2(2\sqrt{6}-1)}{6}.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-1c72eff26ead70d1f9815829398f7534_l3.png)
![\begin{tikzpicture}[yscale=0.4] \draw[thick] (20:2)--(80:2)--(140:2)--(200:2)--(260:2)--(320:2)--(20:2) node[right,midway] {$a$}; \draw (260:2)--(320:2) node[below,midway] {$a$}; \draw (260:2)--(200:2) node[below,midway] {$a$}; \draw[thick,{shift={(0,10)}}] (20:2)--(80:2)--(140:2)--(200:2)--(260:2)--(320:2)--(20:2); \draw[dashed,thick] (140:2)--+(0,10) (80:2)--+(0,10); \draw[thick] (200:2)--+(0,10) (260:2)--+(0,10) (320:2)--+(0,10) (20:2)--+(0,10) node[right,midway] {$h$}; \node[right] at (3,5) {$12\cdot\frac{\sqrt{3}}{4}a^2+6ah=S\sqrt{3}$}; \draw[thin,dashed,blue] (20:2)--(200:2) (140:2)--(320:2) (260:2)--(80:2); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-eca8cf53262e989df0e5b46dc55a262b_l3.png)
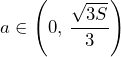 . Objętość
. Objętość ![\[V_{\max}=V\left(\frac{\sqrt{S}}{3}\right)=\frac{S\sqrt{S}}{6}.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-a5f49fa78d6e9380f263947cb16010db_l3.png)
![\begin{tikzpicture}[node distance={35mm}, thick,main/.style = {draw, circle},mm/.style = {draw, rectangle}] \node[mm] (1) {START: $4b+8cz$}; \node[mm] (2) [below left of=1] {$6b+8cz$}; \node[mm] (3) [below right of=1] {$4b+7cz+2z$}; \draw[->] (1) -- node[midway,below, sloped, pos=0.5] {bia{\l}a} (2); \draw[->] (1) -- node[midway,above, sloped, pos=0.5] {$p=\frac{4}{12}$} (2); \draw[->] (1) -- node[midway,below, sloped, pos=0.5] {czarna} (3); \draw[->] (1) -- node[midway,above, sloped, pos=0.5] {$p=\frac{8}{12}$} (3); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-921e22aa87542c9637b8fd3cc3cf12a3_l3.png)
![\[\frac{4}{12}\cdot\frac{\binom{6}{2}}{\binom{14}{2}}+\frac{8}{12}\cdot\frac{\binom{4}{2}}{\binom{13}{2}}=\frac{1}{3}\cdot\frac{15}{91}+\frac{2}{3}\cdot\frac{6}{78}=\frac{29}{273}.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-50a01f1a69c1ad62b38e75b9fb9fdd0f_l3.png)
![\begin{tikzpicture}[scale=1] \coordinate[label=below left:$A$] (A) at (0,0); \coordinate[label=below:$B$] (B) at (3,0); \coordinate[label=above right:$C$] (C) at (4,2); \coordinate[label=left:$D$] (D) at (1,2); \coordinate[label=above left:$E$] (E) at (1,5); \coordinate[label=above right:$F$] (F) at (4,5); \coordinate[label=right:$G$] (G) at (6,1); \coordinate[label=right:$H$] (H) at (5,-1); \draw[thick] (A)--(B)--(C)--(D)--cycle; \draw[thick,blue] (D)--(C)--(F)--(E)--cycle; \draw[thick,red] (B)--(H)--(G)--(C)--cycle; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-bd1186e6ec89576e1c13d2922446a593_l3.png)
![\begin{tikzpicture}[scale=1] \coordinate[label=below left:$A$] (A) at (0,0); \coordinate[label=below:$B$] (B) at (3,0); \coordinate[label=above right:$C$] (C) at (4,2); \coordinate[label=left:$D$] (D) at (1,2); \coordinate[label=above left:$E$] (E) at (1,5); \coordinate[label=above right:$F$] (F) at (4,5); \coordinate[label=right:$G$] (G) at (6,1); \coordinate[label=right:$H$] (H) at (5,-1); \coordinate[label=right:$X$] (X) at (6,4); \draw[thick] (A)--(B)--(C)--(D)--cycle; \draw[thick] (D)--(C)--(F)--(E)--cycle; \draw[thick] (B)--(H)--(G)--(C)--cycle; \draw[very thick,red] (A)--(C) (F)--(G); \draw[blue] (C)--(F)--(X)--(G)--cycle; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6d4120d9512056bda864889f70805a24_l3.png)
![\begin{tikzpicture}[scale=1] \draw (0,0) circle (2cm); \draw[thick] (-4,-2)--(4,-2)--(1,2)--(-1,2)--cycle; \node[below left] at (-4,-2) {$A$}; \node[below right] at (4,-2) {$B$}; \node[above] at (1,2) {$C$}; \node[above] at (-1,2) {$D$}; \draw[blue] (1,2)--(1,-2) node[left,midway] {$2r$}; \node[below] at (1,-2) {$E$}; \draw (1,-2)--(4,-2) node[below,midway,scale=0.8] {$\frac{|AB|-|CD|}{2}$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-375207616c5892a9b77b6c8d57de3957_l3.png)
![\begin{tikzpicture}[scale=1] \draw (0,0) circle (2cm); \draw[thick] (-4,-2)--(4,-2)--(1,2)--(-1,2)--cycle; \node[below left] at (-4,-2) {$A$}; \node[below right] at (4,-2) {$B$}; \node[above] at (1,2) {$C$}; \node[above] at (-1,2) {$D$}; \draw[blue,thick] (1,-2)--(1,2)--(-4,-2); \node[below] at (1,-2) {$E$}; \node[below] at (0,-2) {$a$}; \node[above] at (0,2) {$b$}; \node[right,blue] at (1,0) {$h$}; \draw[blue] (-4,-2)--(1,2) node[above,midway,sloped] {$\sqrt{41}$}; \draw (1,-2)--(4,-2) node[below,midway,scale=0.8] {$\frac{a-b}{2}$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6d87b0d2ba6dce12b727c7b27ea3a194_l3.png)
![\begin{tikzpicture}[scale=1.7] \coordinate[label=below left:$A$] (A) at (180:2); \coordinate[label=below right:$B$] (B) at (0:2); \coordinate[label=above:$C$] (C) at (50:2); \coordinate[label=below:$H$] (H) at ($(A)!(C)!(B)$); \coordinate[label=below:$M$] (M) at (0,0); \draw[thick] (A)--(B)--(C)--cycle; \draw[blue,thick] (H)--(C)--(M); \node[scale=1.1,blue] at ($(C)+(250:0.4)$) {$\alpha$}; \draw (A)--(C) node[above,midway] {$b$}; \draw (B)--(C) node[right,midway] {$a$}; \draw[blue] (C)--(H) node[right,midway] {$h$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-ad66d385d4affa977f374cf3ed71dc8d_l3.png)
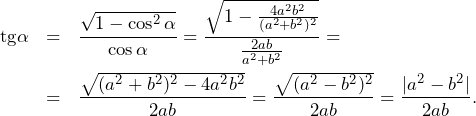
![\begin{tikzpicture} \coordinate[label=below left:$A$] (A) at (200:2); \coordinate[label=below right:$B$] (B) at (340:2); \coordinate[label=above:$C$] (C) at (100:2); \draw[thick] (A)--(B)--(C)--cycle; \draw[thin,blue,shift={(A)}] (0:0.7) arc (0:60:0.7) node at (30:0.44) {$\alpha$}; \draw[thin,blue,shift={(B)}] (130:0.7) arc (130:180:0.7) node at (155:0.5) {$\beta$}; \draw[thin,blue,shift={(C)}] (240:0.7) arc (240:310:0.7) node at (275:0.5) {$\gamma$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-3c601a639de931674ceb00a38b97576a_l3.png)
![\begin{tikzpicture} \coordinate[label=below left:$A$] (A) at (200:2); \coordinate[label=below right:$B$] (B) at (340:2); \coordinate[label=above:$C$] (C) at (100:2); \coordinate[label=above left:$D$] (D) at (160:2); \draw[thick,blue] (A)--(C); \draw[red,thick] (B)--(D); \draw[thin,dashed] (0,0) circle (2cm); \draw[thick] (A)--(B)--(C)--(D)--cycle; \draw[thin,blue,shift={(B)}] (130:0.7) arc (130:180:0.7) node at (155:0.5) {$\beta$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-9d51657d2c5788b6e6702fdfd591b8cb_l3.png)
![\[R=\dfrac{|AC|}{\sin\beta}=\dfrac{5}{\frac{\sqrt{5}}{3}}=3\sqrt{5}.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-cff9c33ded0e69de2372fa51e4351d76_l3.png)
![\begin{tikzpicture}[scale=0.6] \draw[black!30] (-9.5,-7.5) grid (8.5,9.5); \draw[ultra thick,->] (-9.5,0)--(8.5,0) node[below] {$x$}; \draw[very thick,->] (0,-7.5)--(0,9.5) node[left] {$y$}; \coordinate[label=above:$A$] (A) at (-2,5); \coordinate[label=below right:$C$] (C) at (-3,-2); \coordinate[label=below right:$B_1$] (B1) at (2,3); \coordinate[label=below right:$B_2$] (B2) at (-8,-7); \draw[blue] (-9,-8)--(8.5,9.5) node[below,sloped,near end] {$y=x+1$}; \draw[fill=black] (A) circle (0.09cm); \draw[fill=black] (C) circle (0.09cm); \draw[fill=black] (B1) circle (0.09cm); \draw[fill=black] (B2) circle (0.09cm); \draw[red,thick] (A)--(B1)--(C)--cycle; \draw[green!50!black,thick] (A)--(B2)--(C)--cycle; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-5fd4281da2657996bda8f7947d2e8df6_l3.png)
![\begin{tikzpicture}[scale=1.2] \draw[black!30] (-3.5,-1.5) grid (4.8,3.8); \draw[ultra thick,->] (-3.5,0)--(5,0) node[below] {$x$}; \draw[very thick,->] (0,-1.5)--(0,4) node[left] {$y$}; \foreach \x in {-3,-2,-1,1,2,3,4} \draw (\x,0)--(\x,-0.05) node[below] {\bf \x }; \foreach \y in {-1,1,2,3} \draw (0,\y)--(-0.05,\y) node[left] {\bf \y }; \draw[domain=-3.2:-0.5, smooth,thick, variable=\x] plot ({\x}, {1/(\x*\x)}); \draw[domain=0.5:4, smooth,thick, variable=\x] plot ({\x}, {1/(\x*\x)}); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-5ee189987045e55c738c711c6140e7b7_l3.png)
![\[A=\left(-\sqrt{\frac{1}{a}},\,a\right),\quad B=\left(\sqrt{\frac{1}{a}},\,a\right).\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-a7ba13c04e7def153e343f3ba2e943c9_l3.png)
![\begin{tikzpicture}[scale=1.2] \draw[black!40] (-3.5,-1.5) grid (4.8,3.8); \draw[ultra thick,->] (-3.5,0)--(5,0) node[below] {$x$}; \draw[very thick,->] (0,-1.5)--(0,4) node[left] {$y$}; \foreach \x in {-3,-2,-1,1,2,3,4} \draw (\x,0)--(\x,-0.05) node[below] {\bf \x }; \foreach \y in {-1,1,2,3} \draw (0,\y)--(-0.05,\y) node[left] {\bf \y }; \coordinate[label=below right:$C$] (C) at (3,-1); \draw[domain=-3.2:-0.5, smooth,thick, variable=\x] plot ({\x}, {1/(\x*\x)}); \draw[domain=0.5:4, smooth,thick, variable=\x] plot ({\x}, {1/(\x*\x)}); \draw[fill=black] (C) circle (0.07cm); \draw[blue] (-2.5,1.778)--(2.5,1.778) node[above] {$y=a$}; \coordinate[label=above right:$B$] (B) at (0.75,1.778); \draw[fill=blue] (B) circle (0.07cm); \coordinate[label=above left:$A$] (A) at (-0.75,1.778); \draw[fill=blue] (A) circle (0.07cm); \draw[red,thick] (A)--(B)--(C)--cycle; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-cc0df892dba8558237bc9324bf532cbe_l3.png)
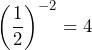 .
.
![\begin{tikzpicture}[scale=0.75] \draw[blue!15,fill=blue!15] (-5,3.4) rectangle (-1,-3.4); \draw[blue!15,fill=blue!15] (5,-3.4) rectangle (1,3.4); \draw[red,ultra thick] (-5,-3.4)--(-5,3.4) (5,-3.4)--(5,3.4); \draw[red,ultra thick,dashed] (-1,-3.4)--(-1,3.4) (1,-3.4)--(1,3.4); \draw[black!40] (-6.5,-3.5) grid (6.5,3.5); \draw[thick,->] (-6.5,0)--(6.5,0) node[below] {$x$}; \draw[thick,->] (0,-3.5)--(0,3.5) node[left] {$y$}; \foreach \x in {-6,-5,-4,-3,-2,-1,1,2,3,4,5,6} \draw (\x,0)--(\x,-0.05) node[below] { \x }; \foreach \y in {-3,-2,-1,1,2,3} \draw (0,\y)--(-0.05,\y) node[left] {\y }; \draw[dashed,ultra thick,red!80] (-5,0)--(-1,0) (1,0)--(5,0); \draw[fill=white] (-5,0) circle (3pt); \draw[fill=white] (5,0) circle (3pt); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-7e733aea74bc70e27212242fc3723ccc_l3.png)
![\begin{tikzpicture}[scale=0.3] \draw[black!30] (-10.5,-8.5) grid (5.5,9.5); \coordinate[label=below left:$A$] (A) at (-9,-2); \coordinate (O) at (-2.5,0); \coordinate[label=above right:$B$] (B) at (4,2); \coordinate[label=above right:$C_1$] (C1) at (0,6.3); \coordinate[label=below right:$C_2$] (C2) at (0,-6.3); \draw[blue] (-2.5,0) circle (6.8) (A)--(B); \draw[thick,->] (-10.5,0)--(5.5,0) node[below] {$x$}; \draw[thick,->] (0,-8.5)--(0,9.5) node[left] {$y$}; \draw[red] (A)--(C1)--(B) (A)--(C2)--(B); \foreach \p in {A,B,C1,C2,O} \draw[fill=black] (\p) circle (4.5pt); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-1195106a4c461782a56cfb64df12d6fd_l3.png)
![\[\left(x+\frac{5}{2}\right)^2+(y-0)^2=\left(\frac{\sqrt{185}}{2}\right)^2=\frac{185}{4}.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-392ed879cbf75cd7ffdbc344689aef21_l3.png)
![\begin{tikzpicture}[scale=1] \draw[black!40] (-7.4,-2.5) grid (7.8,6.8); \draw[ultra thick,->] (-7.5,0)--(8,0) node[below] {$x$}; \draw[ultra thick,->] (0,-2.5)--(0,7) node[left] {$y$}; \foreach \x in {-7,-6,-5,-4,-3,-2,-1,1,2,3,4,5,6,7,} \draw (\x,0)--(\x,-0.05) node[below] {\bf \x }; \foreach \y in {-1,1,2,3,4,5,6} \draw (0,\y)--(-0.05,\y) node[left] {\bf \y }; \draw[domain=0.7:3.2, smooth,thick, blue,variable=\y] plot ({12-6*\y}, {\y}); \draw[domain=-0.9:6, smooth,blue,thick,variable=\y] plot ({7-\y}, {\y}); \draw[domain=2.7:6, smooth,thick, blue,variable=\y] plot ({4*\y-18}, {\y}); \coordinate[label=above:$A$] (A) at (2,5); \coordinate[label=above right:$B$] (B) at (6,1); \coordinate[label=below:$C$] (C) at (-6,3); \coordinate[label=left:$S$] (S) at (-0.6,-1.6); \coordinate[label=left:$M_1$] (M1) at (4,3); \coordinate[label=above left:$M_2$] (M2) at (-2,4); \draw[shift={(-0.6,-1.6)},red,thick] (0:7.09) arc (0:170:7.09); \foreach \w in {A,B,C,S,M1,M2} \draw[fill=black] (\w) circle (1.7pt); \draw[domain=-1.5:6, smooth,thick,dashed,variable=\x] plot ({\x},{\x-1}); \draw[domain=-2.8:-0.2, smooth,thick,dashed,variable=\x] plot ({\x},{-4*\x-4}); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-c75b71e281e080dbe39ff532d201e4d2_l3.png)