Poniżej prezentujemy rozwiązania wszystkich zadań maturalnych z matematyki dla poziomu rozszerzonego, z którymi abiturienci mierzyli się 12. maja 2023 r. Zadania pochodzą z arkusza opublikowanego w serwisie Centralnej Komisji Egzaminacyjnej.
Zadanie 1. (0-1)
Granica ![]() jest równa
jest równa
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 2. (0-1)
Dane są wektory ![]() oraz
oraz ![]() . Długość wektora
. Długość wektora ![]() jest równa
jest równa
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 3. (0-1)
Punkty ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() leżą na okręgu o środku
leżą na okręgu o środku ![]() . Miara kąta
. Miara kąta ![]() jest równa
jest równa ![]() , a miara kąta
, a miara kąta ![]() jest równa
jest równa ![]() (zobacz rysunek).
(zobacz rysunek).
![\begin{tikzpicture}[scale=1.3] \draw (0,0) circle (2cm); \coordinate (A) at (275:2); \coordinate (B) at (345:2); \coordinate (C) at (55:2); \coordinate (D) at (125:2); \coordinate (E) at (200:2); \foreach \x/\w in {A/275,B/345,C/55,D/125,E/200} \draw[fill=black] (\x) circle (1pt) node at (\w:2.28) {$\x$}; \draw[fill=black] (0,0) circle (1pt) node[below right] {$S$}; \draw[thick] (A)--(B)--(C)--(D)--(E)--cycle; \draw (B)--(D)--(A); \draw[thin,shift={(C)}] (180:0.7) arc (180:290:0.7) node[scale=0.75] at (235:0.4) {$110^\circ$}; \draw[thin,shift={(D)}] (290:1.3) arc (290:325:1.3) node[scale=0.8] at (307:1) {$35^\circ$}; \draw[thin,shift={(E)}] (327:0.6) arc (327:432:0.6); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6db04fd5e1281457204b7a8f4133fa3e_l3.png)
A.
B.
C.
D.
Zadanie 4. (0-1)
Dany jest zbiór trzynastu liczb ![]() , z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch
liczb, których iloczyn jest liczbą parzystą, jest
, z którego losujemy jednocześnie dwie liczby. Wszystkich różnych sposobów wylosowania z tego zbioru dwóch
liczb, których iloczyn jest liczbą parzystą, jest
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Zadanie 5. (0-2)
Wielomian ![]() ma dokładnie jeden pierwiastek rzeczywisty.
Oblicz ten pierwiastek.
ma dokładnie jeden pierwiastek rzeczywisty.
Oblicz ten pierwiastek.
W poniższe kratki wpisz kolejno – od lewej do prawej – pierwszą, drugą oraz trzecią cyfrę po przecinku nieskończonego rozwinięcia dziesiętnego otrzymanego wyniku.
![\begin{tikzpicture}[yscale=1.5,scale=0.8] \draw[very thick] (0,0) grid (3,1); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-c5183acb72d252f5924056c98e521912_l3.png)
Zadanie 6. (0-3)
Liczby rzeczywiste ![]() oraz
oraz ![]() spełniają jednocześnie równanie
spełniają jednocześnie równanie ![]() i nierówność
i nierówność
![]() . Wykaż, że
. Wykaż, że ![]() oraz
oraz ![]() .
.
Zadanie 7. (0-3)
Dany jest trójkąt prostokątny ![]() , w którym
, w którym ![]() oraz
oraz ![]() . Punkty
. Punkty ![]() i
i ![]() leżą na bokach – odpowiednio –
leżą na bokach – odpowiednio – ![]() i
i ![]() tak, że
tak, że ![]() (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek ![]() przecina wysokość
przecina wysokość ![]() tego trójkąta w punkcie
tego trójkąta w punkcie ![]() , a ponadto
, a ponadto ![]() .
.
![\begin{tikzpicture}[scale=1.3] \coordinate (A) at (0,4); \coordinate (B) at (0,0); \coordinate (C) at (6.9282,0); \coordinate (K) at (0,1); \coordinate (L) at (1,0); \coordinate (D) at ($(A)!(B)!(C)$); \coordinate (N) at (intersection of B--D and K--L); \foreach \x/\r in {A/{above},B/{below left},C/{below},D/{above right},K/{left},L/{below},N/{right}} \draw[fill=black] (\x) circle (0.8pt) node[\r] {$\x$}; \draw (B)--(D); \draw[thin] (A)--(D) node[midway,above right] {$2$}; \draw[thin] (B)--(L) node[midway,below] {$1$}; \draw[thin] (B)--(K) node[midway,left] {$1$}; \draw[thick] (C)--(B)--(A)--cycle; \draw (K)--(L); \draw[thin,shift={(A)}] (270:0.7) arc (270:330:0.7) node at (300:0.5) {$60^\circ$}; \draw[thin,shift={(D)}] (150:0.5) arc (150:240:0.5) node[scale=2] at (195:0.3) {$\cdot$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-2f0b674b5ab00c414b440467e1a35151_l3.png)
Wykaż, że ![]() .
.
Zadanie 8. (0-3)
W pojemniku jest siedem kul: pięć kul białych i dwie kule czarne. Z tego pojemnika losujemy jednocześnie dwie kule bez zwracania. Następnie – z kul pozostałych w pojemniku – losujemy jeszcze jedną kulę. Oblicz prawdopodobieństwo wylosowania kuli czarnej w drugim losowaniu.
Zadanie 9. (0-3)
Funkcja ![]() jest określona wzorem
jest określona wzorem ![]() dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej ![]() . Punkt
. Punkt ![]() należy do wykresu funkcji
należy do wykresu funkcji ![]() . Oblicz
. Oblicz ![]() oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji ![]() w punkcie
w punkcie ![]() .
.
Zadanie 10. (0-4)
Rozwiąż nierówność
![]()
Zadanie 11. (0-4)
Określamy kwadraty ![]() następująco:
następująco:
• ![]() jest kwadratem o boku długości
jest kwadratem o boku długości ![]()
• ![]() jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu ![]() i dzieli ten bok w stosunku
i dzieli ten bok w stosunku ![]()
• ![]() jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu ![]() i dzieli ten bok w stosunku
i dzieli ten bok w stosunku ![]()
i ogólnie, dla każdej liczby naturalnej ![]()
• ![]() jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu ![]() i dzieli ten bok w stosunku
i dzieli ten bok w stosunku ![]() .
.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg
geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
![\begin{tikzpicture}[scale=1.3] \coordinate (A) at (0,0); \coordinate (B) at (4,0); \coordinate (C) at (4,4); \coordinate (D) at (0,4); \node[below] at (2,0) {$a$}; \node[left] at (0,2) {$a$}; \foreach \x in {1,...,10} { \draw (A)--(B)--(C)--(D)--cycle; \coordinate (A1) at ($(A)!0.25!(B)$); \coordinate (B1) at ($(B)!0.25!(C)$); \coordinate (C1) at ($(C)!0.25!(D)$); \coordinate (D1) at ($(D)!0.25!(A)$); \draw (A1)--(B1)--(C1)--(D1)--cycle; \coordinate (A) at ($(A1)!0.25!(B1)$); \coordinate (B) at ($(B1)!0.25!(C1)$); \coordinate (C) at ($(C1)!0.25!(D1)$); \coordinate (D) at ($(D1)!0.25!(A1)$); } \draw[thick] (0,0)--(4,0)--(4,4)--(0,4)--cycle; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-56c042f0f396eae990eb7cabe9ca71ab_l3.png)
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Zadanie 12. (0-4)
Rozwiąż równanie ![]() w przedziale
w przedziale ![]() .
.
Zadanie 13. (0-4)
Czworokąt ![]() , w którym
, w którym ![]() i
i ![]() , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna ![]() tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem ![]() kąt o mierze
kąt o mierze ![]() , natomiast z bokiem
, natomiast z bokiem ![]() – kąt ostry, którego sinus jest równy
– kąt ostry, którego sinus jest równy ![]() . Oblicz obwód czworokąta
. Oblicz obwód czworokąta ![]() .
.
Zadanie 14. (0-4)
Dany jest sześcian ![]() o krawędzi długości
o krawędzi długości ![]() . Punkt
. Punkt ![]() jest punktem przecięcia
przekątnych
jest punktem przecięcia
przekątnych ![]() i
i ![]() ściany bocznej
ściany bocznej ![]() (zobacz rysunek).
(zobacz rysunek).
![\begin{tikzpicture}[scale=0.9] \coordinate (A) at (0,0); \coordinate (B) at (5,0); \coordinate (C) at (7,2); \coordinate (D) at (2,2); \coordinate (E) at (0,5); \coordinate (F) at (5,5); \coordinate (G) at (7,7); \coordinate (H) at (2,7); \coordinate (S) at (1,3.5); \draw[thick] (A)--(B)--(C)--(G)--(H)--(E)--cycle (F)--(G) (E)--(F)--(B); \draw[thick,dashed] (A)--(D)--(H) (D)--(C); \draw[dotted,thick,black!75] (A)--(H) (E)--(D); \node[below] at (2.5,0) {$6$}; \foreach \x/\r in {A/{below left},B/{below right},C/right,D/{below right},E/left,F/right,G/{above right},H/above,S/left} \draw[fill=black] (\x) circle (1pt) node[\r] {$\x$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-7971549f258193790573f1f2e81614a8_l3.png)
Zadanie 15. (0-5)
Wyznacz wszystkie wartości parametru ![]() , dla których równanie
, dla których równanie
![]()
Zadanie 16. (0-7)
Rozważamy trójkąty ![]() , w których
, w których ![]() ,
, ![]() , gdzie
, gdzie ![]() , a wierzchołek
, a wierzchołek ![]() leży na prostej o równaniu
leży na prostej o równaniu ![]() . Na boku
. Na boku ![]() tego trójkąta leży punkt
tego trójkąta leży punkt
![]() .
.
a) Wykaż, że dla ![]() pole
pole ![]() trójkąta
trójkąta ![]() , jako funkcja zmiennej
, jako funkcja zmiennej ![]() , wyraża się wzorem
, wyraża się wzorem
![]()
b) Oblicz tę wartość ![]() , dla której funkcja
, dla której funkcja ![]() osiąga wartość najmniejszą. Wyznacz równanie prostej
osiąga wartość najmniejszą. Wyznacz równanie prostej ![]() , przy której funkcja
, przy której funkcja ![]() osiąga tę najmniejszą wartość.
osiąga tę najmniejszą wartość.
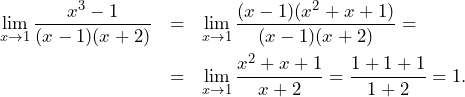
![\begin{tikzpicture}[scale=1.3] \draw (0,0) circle (2cm); \coordinate (A) at (275:2); \coordinate (B) at (345:2); \coordinate (C) at (55:2); \coordinate (D) at (125:2); \coordinate (E) at (200:2); \foreach \x/\w in {A/275,B/345,C/55,D/125,E/200} \draw[fill=black] (\x) circle (1pt) node at (\w:2.28) {$\x$}; \draw[fill=black] (0,0) circle (1pt) node[left] {$S$}; \draw[thick] (A)--(B)--(C)--(D)--(E)--cycle; \draw (B)--(D)--(A); \draw[thin,shift={(C)}] (180:0.7) arc (180:290:0.7) node[scale=0.75] at (235:0.4) {$110^\circ$}; \draw[thin,shift={(D)}] (290:1.3) arc (290:325:1.3) node[scale=0.8] at (307:1) {$35^\circ$}; \draw[thin,shift={(E)}] (327:0.6) arc (327:432:0.6); \draw[blue] (A)--(0,0)--(B) (B)--(0,0)--(D); \draw[thin,shift={(E)}] (327:0.6) arc (327:432:0.6); \draw[thin,red] (275:0.5) arc (275:345:0.5) node[red,scale=0.8] at (310:0.35) {$70^\circ$}; \draw[thin,red] (345:0.4) arc (345:485:0.4) node[red,scale=0.7] at (55:0.23) {$140^\circ$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-a92854f5ea19a24185ce2f283a863a94_l3.png)
![\begin{tikzpicture}[scale=1.3] \coordinate (A) at (0,4); \coordinate (B) at (0,0); \coordinate (C) at (6.9282,0); \coordinate (K) at (0,1); \coordinate (L) at (1,0); \coordinate (D) at ($(A)!(B)!(C)$); \coordinate (N) at (intersection of B--D and K--L); \foreach \x/\r in {A/{above},B/{below left},C/{below},D/{above right},K/{left},L/{below},N/{right}} \draw[fill=black] (\x) circle (0.8pt) node[\r] {$\x$}; \draw (B)--(D); \draw[thin] (A)--(D) node[midway,above right] {$2$}; \draw[thin] (B)--(K) node[midway,left] {$1$}; \draw[thick] (C)--(B)--(A)--cycle; \draw (K)--(L); \draw[thin,shift={(A)}] (270:0.7) arc (270:330:0.7) node at (300:0.5) {$60^\circ$}; \draw[thin,shift={(D)}] (150:0.5) arc (150:240:0.5) node[scale=2] at (195:0.3) {$\cdot$}; \coordinate (P) at ($(B)!(N)!(L)$); \draw[fill=blue!20] (B)--(N)--(P)--cycle; \draw[red] (N)--(P) node[below] {$P$}; \draw[thin,red] (N)--(P) node[right,midway,scale=0.7] {$x$}; \draw[thin,red] (L)--(P) node[above,midway,scale=0.7] {$x$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-886f944440d9d8ed184e6c23f8af632c_l3.png)
![\begin{tikzpicture}[scale=1.3,sibling distance=25mm, level distance=20mm] \node {$(5b+2c)$} child {node {$(3b+2c)$} child {node {$b$}} child {node {$c$}}} child {node {$(4b+1c)$} child {node {}} child {node {$b$}}} child {node {$(5b)$} child {node {}} child {node {$c$}} }; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-622ec857167a83c62d00ae6828efca43_l3.png)
![\[p_1=\frac{\binom{5}{2}}{\binom{7}{2}}=\frac{10}{21},\quad p_2=\frac{\binom{5}{1}\binom{2}{1}}{\binom{7}{2}}=\frac{10}{21},\quad p_3=\frac{\binom{2}{2}}{\binom{7}{2}}=\frac{1}{21}.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6da02ff4cda534b47943cc3970f0bb96_l3.png)
![\begin{tikzpicture} \draw[very thick, ->] (-3.5,0)--(3.9,0) node[below] {$x$}; \foreach \x in {-2,0,3} \draw (\x,0)--(\x,-0.07) node[below] {$\x$}; \draw[thin,blue] (-3.2,0.4)--(-2.2,0.4)--(-2,0.05)--(-1.8,0.4)--(2.8,0.4)--(3,0.05)--(3.2,0.4)--(3.8,0.4); \node[above,red,scale=1.3] at (-2.7,0.3) {$1^\circ$}; \node[above,red,scale=1.3] at (0.5,0.3) {$2^\circ$}; \node[above,red,scale=1.3] at (3.5,0.3) {$3^\circ$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-35b3bffe486210721d3bfb6ba9070a3a_l3.png)
![\[S=\frac{r_1}{1-q}=\frac{4a}{1-\frac{\sqrt{10}}{4}}=\frac{16}{4-\sqrt{10}}a=\frac{8(4+\sqrt{10})}{3}a.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-0a94334c98c6aec62d0d85b35b011758_l3.png)
![\begin{tikzpicture}[scale=0.65] \coordinate (A) at (-7.32,4.94); \coordinate (B) at (6.46,6.56); \coordinate (C) at (7.97,2.85); \coordinate (D) at (5.97,-1.73); \coordinate (O) at (4.3,2.9); \foreach \x/\w in {A/left,B/above,C/right,D/below} \draw[fill=black] (\x) circle (1pt) node[\w] {$\x$}; \draw[blue] (A)--(C); \draw[thin] (B)--(C) node[midway,right] {$4$}; \draw[thin] (D)--(C) node[midway,right] {$5$}; \draw[thin] (B)--(A) node[midway,above] {$a$}; \draw[thin] (D)--(A) node[midway,below] {$b$}; \draw[thin,shift={(A)}] (352:3) arc (352:366.5:3) node at (360:2.3) {$\alpha$}; \draw[thin,shift={(C)}] (472:1.4) arc (472:532:1.4) node at (501:0.9) {$60^\circ$}; \draw[thick] (A)--(B)--(C)--(D)--cycle; \draw[red] (O) circle (3.387cm); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-743b65edb950204a509aa81d6e247292_l3.png)
![\begin{tikzpicture}[scale=0.9] \coordinate (A) at (0,0); \coordinate (B) at (5,0); \coordinate (C) at (7,2); \coordinate (D) at (2,2); \coordinate (E) at (0,5); \coordinate (F) at (5,5); \coordinate (G) at (7,7); \coordinate (H) at (2,7); \coordinate (S) at (1,3.5); \coordinate (K) at ($(B)!(S)!(H)$); \draw[fill=yellow!30] (A)--(B)--(G)--(H)--cycle; \draw[fill=blue!30] (S)--(B)--(H)--cycle; \draw[red,thick] (S)--(K) node[below right,midway] {$d$}; \draw[thick] (A)--(B)--(C)--(G)--(H)--(E)--cycle (F)--(G) (E)--(F)--(B); \draw[thick,dashed] (A)--(D)--(H) (D)--(C); \draw[dotted,thick,black!75] (A)--(H) (E)--(D); \node[below] at (2.5,0) {$6$}; \foreach \x/\r in {A/{below left},B/{below right},C/right,D/{below right},E/left,F/right,G/{above right},H/above,S/left} \draw[fill=black] (\x) circle (1pt) node[\r] {$\x$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-4e76ba7ad62cd979b06e96275aef6685_l3.png)
![\begin{tikzpicture}[scale=1] \coordinate (A) at (0,0); \coordinate (B) at (6,0); \coordinate (D) at (3,2); \coordinate (C) at (-3,6); \draw[fill=yellow!40] (A)--(B)--(C)--cycle; \draw[black!70] (-6.4,-1.2) grid (6.3,8.3); \draw[very thick,->] (-6.4,0)--(6.3,0) node[below] {$x$}; \draw[very thick,->] (0,-1.2)--(0,8.3) node[left] {$y$}; \draw[thick,blue,dashed] (-4.3,8.6)--(1,-2) node[below,sloped,midway] {$y=-2x$}; \draw[very thick,brown,dashed] (4,-1.2)--(4,8.3); \foreach \x in {A,B,D,C} \draw[fill=black] (\x) circle (1.7pt) node[below left] {$\x$}; \node[below left] at (4,0) {$4$}; \node[above] at (B) {$(m,0)$}; \node[above] at (D) {$(3,2)$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-e9f93e7a2397370367fb95608694c52d_l3.png)
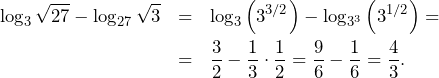
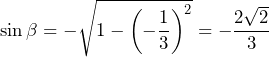 . Mamy też
. Mamy też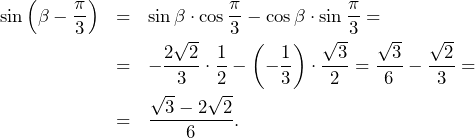
![\begin{tikzpicture}[scale=0.9] \coordinate[label=below left:$A$] (A) at (200:3); \coordinate[label=below right:$B$] (B) at (340:3); \coordinate[label=above:$C$] (C) at (2,4); \coordinate[label=above:$D$] (D) at (-1.2,4); \coordinate[label=right:$P$] (P) at (intersection of A--C and B--D); \draw (C)--(D) node[above,midway] {$a$}; \draw (A)--(B) node[below,midway] {$a+2$}; \draw[thick] (A)--(C); \draw[thick] (B)--(D); \draw[thick] (A)--(B)--(C)--(D)--cycle; \draw[thin,blue,shift={(P)}] (46:0.6) arc (46:127:0.6) node at (88:0.4) {$\alpha$}; \draw[thin,blue,shift={(P)}] (226:0.6) arc (226:307:0.6) node at (268:0.4) {$\alpha$}; \node at (0.35,3.4) {$R$}; \node at (0.2,0.2) {$R+3$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-5dac939cc3c74eeb464f01438fa2b051_l3.png)
![\begin{tikzpicture}[scale=1.2,yscale=1] \draw[thin,fill=red!20] (-1,0) rectangle (0,0.4); \draw[red!20,thin,fill=red!20] (3,0) rectangle (3.9,0.4); \draw (3,0)--(3,0.4)--(3.9,0.4) ; \draw[thick,blue,domain=-1.7:3.3, smooth, variable=\x,yscale=0.2] plot ({\x},{(\x+1)*(\x+0)*(\x-3)}); \draw[very thick,->] (-1.8,0)--(4,0) node[below] {$x$}; \foreach \x/\w in {-1/{-1},0/{-\frac{1}{2}},3/3} { \draw (\x,0)--(\x,-0.06) node[below] {$\w$}; \draw[fill=black] (\x,0) circle (2pt);} \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-a971ee5d2cd14b5e06868d8ce48b2612_l3.png)
![\begin{tikzpicture}[scale=1.5] \draw[fill=blue!20,blue!20] (0,3.5)--(2,0)--(3,4.9); \draw[thick,dashed] (0,0)--(2,0)--(3,1.4)--(1,1.4)--cycle (1,1.4)--(1,4.9); \draw[thick] (0,0)--(2,0)--(3,1.4); \draw[thick,shift={(0,3.5)}] (0,0)--(2,0)--(3,1.4)--(1,1.4)--cycle; \draw[thick] (0,0)--(0,3.5) (2,0)--(2,3.5) (3,1.4)--(3,4.9); \draw[blue,thick] (0,3.5)--(2,0)--(3,4.9); \foreach \x/\y/\g/\w in {0/0/{below left}/D,2/0/{below right}/A,3/1.4/right/B,1/1.4/left/C, 0/3.5/{left}/H,2/3.5/{below right}/E,3/4.9/above/F,1/4.9/above/G } \node[\g] at (\x,\y) {$\w$}; \draw[thick,blue,shift={(2,0)}] (77:0.7) arc (77:120.5:0.7) node[black] at (99:0.55) {$\alpha$}; \node[left] at (0,1.75) {$h$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-ce47164bc74c45da52972417695ac07d_l3.png)
![\begin{tikzpicture}[scale=1.5] \draw (0,0)--(1,-4) node[left,midway] {$\sqrt{a^2+h^2}$}; \draw (3,0)--(1,-4) node[right,midway] {$\sqrt{b^2+h^2}$}; \draw (0,0)--(3,0) node[above,midway] {$\sqrt{a^2+b^2}$}; \draw[blue,thick,fill=blue!20] (0,0)--(3,0)--(1,-4)--cycle; \foreach \x/\y/\g/\w in {0/0/{above left}/H,3/0/{above right}/F,1/-4/below/A} \node[\g] at (\x,\y) {$\w$}; \draw[thick,blue,shift={(1,-4)}] (64:0.6) arc (64:105:0.6) node[black] at (84:0.4) {$\alpha$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-cbe0ef1ac00f092b63a39ff167ba5121_l3.png)
![\begin{tikzpicture}[scale=0.5] \draw[black!30] (-10.5,-9.5) grid (10.5,9.5); \draw[ultra thick,->] (-10.5,0)--(10.5,0) node[below] {$x$}; \draw[very thick,->] (0,-9.5)--(0,9.5) node[left] {$y$}; \coordinate[label=above:$A$] (A) at (-3,2); \coordinate[label=below right:$C$] (C) at (4,3); \coordinate[label=below right:$B_1$] (B1) at (9,8); \coordinate[label=left:$B_2$] (B2) at (-1,-2); \draw[blue] (-8,-9)--(10.5,9.5) node[below,sloped,near start] {$y=x-1$}; \draw[fill=black] (A) circle (0.09cm); \draw[fill=black] (C) circle (0.09cm); \draw[fill=black] (B1) circle (0.09cm); \draw[fill=black] (B2) circle (0.09cm); \draw[red,thick] (A)--(B1)--(C)--cycle; \draw[green!50!black,thick] (A)--(B2)--(C)--cycle; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-cb804ffffc8d9f294cfe3e78e0d8690b_l3.png)
![\begin{tikzpicture}[scale=1.4] \draw[thick](0,0)--(2,0)--(1,3)--cycle; \draw[thick,blue] (1,3)--(1,0); \node[left,blue] at (1,1.2) {$h$}; \node[below] at (1,0) {$a$}; \draw (0,0)--(1,3) node[left,midway] {$b$}; \draw (2,0)--(1,3) node[right,midway] {$b$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6567a63e847aa0c476b4e9175606affb_l3.png)
![\begin{eqnarray*} \left(\log_{\frac{1}{x}}y\right)\cdot \left(\log_{\frac{1}{y}}x\right)&=&\frac{1}{\log_y\frac{1}{x}}\cdot\frac{1}{\log_x\frac{1}{y}}=\nonumber\\[0.25cm] &=&\left(-\frac{1}{\log_yx}\right)\cdot\left(-\frac{1}{\log_xy}\right)=\nonumber\\[0.25cm] &=&\frac{1}{\log_yx}\cdot\log_yx=1.\nonumber \end{eqnarray*}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-91eeeb58eea09a7ea4b875f55c8bf5fc_l3.png)
![\begin{tikzpicture}[scale=0.8] \draw[black!70] (-5.1,-2) grid (7.1,6); \draw[very thick,->] (-5.1,0)--(7.1,0) node[below] {$x$}; \draw[very thick,->] (0,-2)--(0,6) node[right] {$y$}; \foreach \x in {-5,...,7} \draw[thin] (\x,0.15)--(\x,-0.15) node[below,scale=0.8] {\bf \x}; \foreach \x in {-1,1,2,3,4,5} \draw[thin] (0.15,\x)--(-0.15,\x) node[left,scale=0.8] {\bf \x}; \coordinate[label=above right:$D$] (D) at (-4,3); \coordinate[label=below left:$A$] (A) at (-1,0); \coordinate[label=above:$B$] (B) at (1,2); \coordinate[label=below right:$C$] (C) at (3,0); \coordinate[label=above left:$E$] (E) at (6,3); \draw[blue,very thick] (-5.1,4.1)--(A)--(B)--(C)--(7,4); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-6090511fbc4032496bb53adbb2be5015_l3.png)
![\begin{tikzpicture} \coordinate[label=below left:$A$] (A) at (0,0); \coordinate[label=below right:$B$] (B) at (7,0); \coordinate[label=above:$C$] (C) at (3.5,6); \coordinate[label=above left:$M$] (M) at ($(A)!0.3!(C)$); \coordinate[label=above right:$N$] (N) at ($(C)!0.3!(B)$); \coordinate[label=below:$S$] (S) at ($(A)!(M)!(B)$); \coordinate[label=below:$T$] (T) at ($(A)!(N)!(B)$); \coordinate[label=below:$P$] (P) at (3.5,0); \coordinate[label=left:$K$] (K) at ($(C)!(N)!(P)$); \draw[thick] (A)--(B)--(C)--cycle (S)--(M) (T)--(N); \draw[thick,blue] (C)--(P); \draw[very thick, red] (A)--(S) (P)--(T) (N)--(K); \foreach \p in {A,B,C,M,N,S,T,P,K} \draw[fill=black!70] (\p) circle (0.03cm); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-ae1676ffe394e51b833408d853aea8be_l3.png)
![\begin{tikzpicture} \coordinate[label=below left:$A$] (A) at (180:7); \coordinate[label=below right:$B$] (B) at (0,0); \coordinate[label=above:$C$] (C) at (130:5); \coordinate[label=below:$D$] (D) at (180:5); \draw[thick] (A)--(B)--(C)--cycle (C)--(D); \draw[thin] (C)--(D) node[midway,right] {$14$}; \draw[thin] (C)--(A) node[midway,left] {$16$}; \draw[thin] (C)--(B) node[midway,right] {$x$}; \draw[thin] (B)--(D) node[midway,below] {$x$}; \draw[thin] (A)--(D) node[midway,below] {$6$}; \foreach \p in {A,B,C,D} \draw[fill=black!70] (\p) circle (0.03cm); \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-f6988d20bddece75cfa8dd873f2bdae5_l3.png)
![\begin{tikzpicture}[scale=0.4] \draw[black!70] (-6,-12) grid (17,9); \draw[very thick,->] (-6,0)--(17,0) node[below] {$x$}; \draw[very thick,->] (0,-12)--(0,9) node[left] {$y$}; \foreach \x in {-2,2,4,...,12,14} \draw[thin] (\x,0.25)--(\x,-0.25) node[below,scale=0.7] {\bf \x}; \foreach \x in {-10,-8,...,-2,2,4} \draw[thin] (0.25,\x)--(-0.25,\x) node[left,scale=0.7] {\bf \x}; \draw[blue,thick] (6,4) circle (3cm); \draw[dashed,red,very thick] (-5.5,-2)--(16.5,-2); \draw[red,thick] (6,-2) circle (9cm); \draw[very thick, green!80!black,shift={(-4.39,-2)}] (-60:9) arc (-60:90:9); \draw[very thick, green!80!black,shift={(16.39,-2)}] (95:9) arc (95:195:9); \draw[fill=black!70,thick] (-4.39,-2) circle (0.1cm) node[below,scale=0.9] {$a=6-6\sqrt{3}$}; \draw[fill=black!70,thick] (16.39,-2) circle (0.1cm) node[below,scale=0.9] {$a=6+6\sqrt{3}$}; \draw[fill=black!70,thick] (6,-2) circle (0.1cm) node[below,scale=0.9] {$a=6$}; \draw[fill=black!70,thick] (6,4) circle (0.1cm) node[right,scale=0.8] {$(6,4)$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-08b0feb426c87e606eb316facbc476a0_l3.png)
![\[\left(\frac{2}{3\cdot\frac{a+c}{2}}\right)^2=\frac{1}{a}\cdot\frac{1}{2a+a+c+c}.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-00229c6cbe2ec902202ee4ef30492f12_l3.png)
![\[9(t+1)^2=16t(3t+2)\quad\Leftrightarrow\quad $39t^2+14t-9=0.\]](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-f730588fb60cf58f457512670a6d5169_l3.png)
![\begin{tikzpicture}[yscale=0.15] \draw[thick,->] (-5,0) -- (4,0) node[above right] {$x$}; \draw[domain=-3.2:2.3,smooth,variable=\x,blue,thick] plot ({\x},{2*\x*\x*\x+3*\x*\x-11*\x-6}); \foreach \x/\w in {-3/-3,-0.5/{-\frac{1}{2}},2/2} \node[below] at (\x,0) {$\w$}; \end{tikzpicture}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-70c9e7427f2fc284f23cdc4c03320322_l3.png)
![\begin{eqnarray*} &{}&\sin\left(x-\dfrac{\pi}{3}\right)+\sin\left(x+\dfrac{\pi}{3}\right)=\nonumber\\[0.25cm] &=&\sin x\cos\frac{\pi}{3}-\cos x\sin\frac{\pi}{3}+\sin x\cos\frac{\pi}{3}+\cos x\sin\frac{\pi}{3}=\sin x. \end{eqnarray*}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-8a8b6b91c9ab3f73e2f60b2558dfda78_l3.png)
![\begin{eqnarray*} f(x)&=&\frac{\sqrt{3}}{2}x^2+\frac{8\sqrt{3}}{x}=\frac{\sqrt{3}}{2}\left(x^2+\frac{16}{x}\right)\geqslant\nonumber\\[0.25cm] &\geqslant&\frac{\sqrt{3}}{2}\cdot 12=6\sqrt{3}.\nonumber \end{eqnarray*}](http://bak.maszt.pl/wp-content/ql-cache/quicklatex.com-e471afbf8b2592406ce9f35a0747cec8_l3.png)